私が最初に覚えた数式がラジオの同調回路を表す以下の公式です。この詳細は本連載「三角関数・三角比との出会い」で述べました。
今回は私がラジオ少年だった時代にさかのぼり、電気回路と三角関数との関係についてお話したいと思います。
目次

ラジオ作りに熱中していた小学校5年生の私は、この公式から多くを学びとりました。その最大の収穫は電気と数学のリアリティです。
電気はそれ自体見えません。しかし電気というエネルギーは電気回路を通して光や音に変換されることで、わたしたちは電気の存在を実感することができます。
いかに電気回路を作るかに人の意図が反映されます。
ラジオ少年時代の思い出
私は高性能なラジオを手に入れるために電気回路の仕組みを学び始めました。手にした本を開いてまず驚いたのは数式だらけなことでした。
電気の仕組みを理解するために数学が必要であることを悟った私は、数学も独学で学び始めました。
10歳の少年にとって、公式に現れるπや√記号は初めて接する数学の世界です。なぜラジオに円周率πが現れるのか、疑問を抱きながらも公式を信じてパーツの数値を計算します。それを秋葉原から購入し、半田ごてを握り、回路どおりにラジオを組み立てます。
はたして、公式の計算どおりに選局できるではありませんか。その事実を目の当たりにして、数学の圧倒的な威力を思い知ることになったのです。
私が感動したのは、電気と数学のあまりにも見事な関係でした。このとき私は自分の感動が後にさらに大きな感動になってかえってくることなど思いもよりませんでした。
すべては三角関数からはじまる
電気は大きく分けて「直流」と「交流」の2種類あります。
乾電池が直流電流であるのに対して、コンセントから取り出されるのが100ボルトの交流電流です。乾電池と抵抗器を電線で結んでできるのが直流回路の基本です。
乾電池の電圧をV[ボルト]、抵抗器の抵抗値をR[オーム]、そして回路に流れる電流をI[アンペア]とすれば、V=IRの関係が成り立ちます。オームの法則です。
電気回路を構成する基本的パーツは抵抗器の他にコンデンサーCとコイルLがありますが、これらは直流回路よりも交流回路においてその特徴を見ることができます。
共振現象と呼ばれるもので、直流回路には見られない交流回路特有の現象です。共振現象を出現させる基本回路がLC回路です。
コイルは磁場にエネルギーを蓄え、コンデンサーは電場にエネルギーを蓄えることができます。
コイルとコンデンサーをつないだ回路をつくるとその間をエネルギーが電気(正確には電荷)に変換され行ったり来たりする振り子のような現象がおきます。これが電気回路の共振現象です。
LC共振回路は発振回路(交流をつくる回路)やフィルタ回路(特定の周波数成分を取り出す回路)そしてチューナーなどに応用されます。
最初にあげた公式のfはLC共振回路の共振周波数です。この公式の導出過程の風景を眺めていくときに、先に述べた感動が押し寄せてくることになります。
交流回路にも直流回路のようなオームの法則が成り立つのですが、これがやっかいです。なにせ電気は目に見えないのですから。かといって電気を体で直接確かめるわけにもいきません。
この状況を救う唯一の方法が数学です。
その物語は交流を三角関数で表すことからはじまります。そして必要になる道具が微分積分法です。
共振現象は振り子のようだと説明しましたが、周波数とは1秒当たり繰り返される回数のことで、単位はHz(ヘルツ)です。
交流回路を説明する基本要素が時間です。コイルとコンデンサーに蓄えられるエネルギーは時間とともに変化します。
コイルとコンデンサーに係る電圧や電流は時間の変数として表されるので、時間による微分と積分を使うことでうまく説明できます。
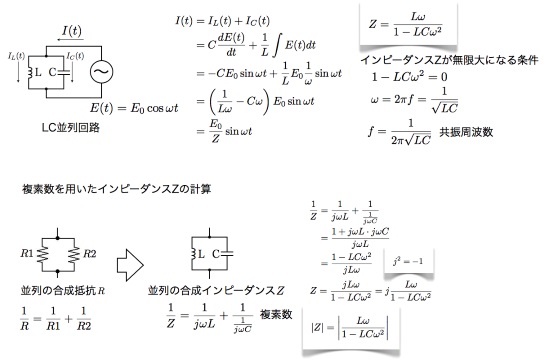
このことを高校物理で学びました。
冒頭の公式を知ってから7年後、三角関数と微分積分法によって見事に交流回路は説明され、同時に公式の証明も手にすることができました。
小学生のときには思いもしなかった感慨無量の瞬間でした。
異端児オリヴァー・ヘヴィサイドの登場
さらなる大きな感動がやってきます。
交流回路の計算の風景は、三角関数にはじまり三角関数に終わる計算です。しかし、これは骨の折れる面倒な計算の連続です。ここに革新の根源がありました。
複雑な三角関数を用いた交流回路の計算を劇的に簡単に行う画期的計算法が見つかります。複素数の出番です。
抵抗、コイル、コンデンサに交流電流が流れると位相がずれることが交流回路の計算の本質でもあり面倒になる原因でもあるのですが、複素数を用いることでこの両方──位相と面倒な計算──が同時に解決します。
それを考え出したのが孤高の電気技師オリヴァー・ヘヴィサイド(1850~1925)です。
イギリスで生まれたヘヴィサイドは16歳で学校をやめ、独学で数学と電気工学を学び電信会社に就職し、通信士の仕事を行います。
24歳で会社をやめ、ロンドンの両親のもと自宅で研究をつづけ電気工学、電磁気学、数学、物理学に数多くの業績を残しました。
コイルにおける自己誘導および相互誘導の大きさを表す量をインダクタンスL(単位H(ヘンリー))といい、交流回路における直流回路の抵抗R(レジスタンス)に相当する量をインピーダンスZと呼びます。これらの用語はヘヴィサイドによって名付けられました。
虚数は数学では記号としてiが用いられますが、電気ではiは電流を表すので虚数にはjが用いられます。
すると、図のようにインピーダンスは即座に表すことができ、先ほどのLC共振回路のような計算もあっという間に完了してしまいます。まさに雷に打たれる思いをしました。
ヘヴィサイドはこの他にも電気工学から新しい数学を導き出しています。現在、ラプラス変換と呼ばれているものはヘヴィサイドによるアイディアです。
先にも述べたように電気回路には時間を変数とする微分積分法が登場します。それは微分方程式という形となり現れてきます。
交流回路における複素数の魔術と同じことを、ヘヴィサイドは微分方程式の解法にももたらしたのです。面倒な微分・積分の計算を掛け算・割り算に変換し簡単に解いてしまう魔法です。
ネイピアによる対数の発見を想起させます。
星と人とともにある数学の金字塔がネイピアの対数の発見でした。それがにオイラーによる微分積分法に続いていったことは本連載で述べてきた通りです。
ヘヴィサイドは星と人とともにつくられてきた数学の新天地を見つけたのです。それが電気の世界だったのです。
電気回路は英語でcircuitですが、ラテン語のcircuitus(丸く回ること)を語源としています。
星の形と軌道が丸いことから生まれた三角関数は、実に長い年月を経て19世紀に電気回路という丸の中に現れてきました。そして、そこからオイラーによる微分積分法と複素数が電気回路の中でさらに進化を遂げていくことになったのです。
この他にもヘヴィサイドは同軸ケーブルを発明し、マクスウェルの電磁場方程式を今日の4つの形にまとめることもしています。
さらに、なぜまっすぐにしか進まない電磁波が地球では曲がって進むのかという問いに、電離層の存在を予想をしたのもヘヴィサイドです。
20世紀以降今日まで電気の時代が続いています。その礎がヘヴィサイドの理論によって支えられているといっても過言ではありません。
星の世界そして電気の世界によって私は数学の絶大な威力を思い知らされたということです。
厳密な数学は狭く、物理的な数学は奔放で広い
(ヘヴィサイド)
