目次
関数電卓を手にする
関数電卓(写真左上)の表示こそ、計算の旅の出発風景でした。
ラジオ作りに熱中していた10歳の私は、電気回路計算のために関数電卓を初めて手にしました。
テンキーと四則以外よくわからない略語が記されたキーが整然と並ぶ様子に、興奮を覚えました。いったい何のためにどんな計算をしてくれるキーなのか、ワクワクしました。
関数電卓で遊ぶようになり、sinキーの意味がわかりはじめました。
「三角比」と呼ばれ、直角三角形の2辺の比の組合せで3通りの三角比「sin(サイン)」「cos(コサイン)」「tan(タンジェント)」があることを知りました。
まず計算してみたのは、3つの角度が30°、60°、90°の三角定規です。
辺の長さを測ると、斜辺が2、高さが1です。これとsinの定義から、sin30°=1/2=0.5がわかります。はたして、関数電卓で30→sinとキーをたたくと0.5と表示されます。
「なるほど!」
新しいことを知り、理解していくことが面白くてなりませんでした。三角定規と関数電卓という2つのアイテムが計算によって繋がっていることを感じ取った瞬間でした。
「ならば、sin31°は?」
31→sin とキーをたたくと、現れた数字が「0.515038074」。私の頭の中には31°、59°、90°の直角三角形が浮かんできました。「31°の直角三角形の斜辺と高さの比が0.5150・・。
でも、この関数電卓は斜辺と高さをいったいどうやって知ることができるのだろう?」ここで思考が中断しました。どうやってもわかりません。
今になって思えば、この鮮烈な経験のおかげで私は数値計算に強い関心を持つようになったのです。
この謎解きの計算の旅の続きは次回以降に譲るとして、原点であるラジオ製作の風景を眺めていきたいと思います。
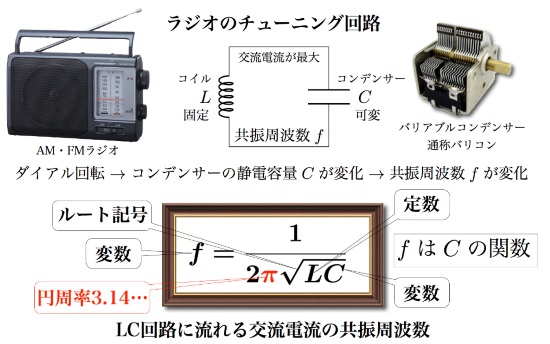
ラジオのチューニング回路
ラジオのチューニングの仕組みはLC共振回路で説明されます(下図)。
Lはコイル、Cはコンデンサーのことです。LC共振回路に流れる交流電流の周波数を変化させると、電流の大きさも変化します。
電流の大きさが最大になる交流電流の周波数を共振周波数と呼びます。そして、共振周波数がラジオの周波数と一致することが「チューニングが合う」「同調」を意味します。
共振周波数fはLとCの数値によって決まることを表すのが下図の数式です。
これこそ人生初の暗記公式です。わけがわからないからまずは覚えたということです。次のことがわかりませんでした。
- ルート記号√の意味
- なぜ円周率πが含まれているのか
- そもそもなぜ共振周波数がこの数式で表されるのか
しかし、理屈がわからなくとも計算できればラジオ製作に役立ちます。
コイルのインダクタンスL[H]を固定(定数)として、コンデンサーの静電容量C[F]を変化させれば共振周波数fも変化する関係は理解できました。
そのためにもまず理解しなくてはいけないのが、√の計算でした。
関数電卓は数学教師
電卓の√キーを押してみると次のようになります。
1 → √ → 1
2 → √ → 1.414213561
3 → √ → 1.732050806
4 → √ → 2
5 → √ → 2.236067977
6 → √ → 2.449489741
7 → √ → 2.645751309
8 → √ → 2.828427122
9 → √ → 3
10 → √ → 3.162277658
1、4、9といった整数に対しては、それぞれ1、2、3という整数値が返ってきます。このパターンから16だったら4、25だったら5、36だったら6と予想できました。
こうして〝x→ √ → y〟は〝y×y=x〟のことではないかと理解するのに、ものの10分もかかりませんでした。
2 → √ → 1.414213561 ⇨ 1.414213561×1.414213561=1.999999996 ≒ 2
このことから、1.414213561という数値は√2の本当の値ではなくそれに近い値(近似値)であることもわかりました。
まさに関数電卓はキーを叩けば叩くほど色々なことを教えてくれる数学教師でした。
かくしてこの7年後、17歳のときに謎2と3の「最初の」謎解きができました。
その証明に現れたものこそ三角関数です。
この共振周波数の公式の証明もまた長い計算の旅になっていくことを、17歳の私は知る由もありませんでした。
私にとってラジオ製作とは、「sin31°」「共振周波数の公式の証明」という計算の旅の誘いだったのです。