目次
三角関数とは
三角関数とは関数の1つで、「平面三角法における、角の大きさと線分の長さの関係を記述する関数の族および、それらを拡張して得られる関数の総称」(出典:Wikipedia)とされています。
90°未満の角度を扱う場合は、三角関数の値は対応する直角三角形の二辺の長さの比であり、三角関数は「三角比」と呼ばれます。
一般に知られている三角関数は以下の3種類です。
- サイン(sin)
- コサイン(cos)
- タンジェント(tan)
これらが三角関数の基本であることは、1つの直角三角形の2辺の組合せが3種類あるからに他なりません。
ここ二千年の間、わたしたちは三角関数とともに地球に生きて文明を築いてきました。
それは地図、航海術、天文学、測地学、測量、物理学、電子工学そして数学といった世界を語る言葉が三角関数だったからです。
わたしたちは、この世界が三角関数によって計算・説明されることを二千年かけて理解してきたということです。その発展の過程で様々な三角関数が考案されてきました。
今回のコラムではサイン(sin)、コサイン(cos)、タンジェント(tan)以外の三角関数、三角関数ファミリーをご紹介しましょう。
三角関数ファミリー
三角関数の逆数
xの逆数とは1/xのことをいいます。
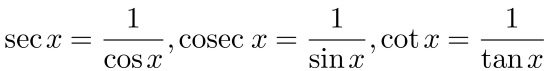
secは正割関数(secant:セカント)、cosecは余割関数(cosecant:コセカント)、cotは余接関数(cotangent:コタンジェント)と読みます。
三角関数の逆関数
関数y=f(x)とは、xに対してyが対応することを意味します。このとき、yに対してxが対応する関数を考えることができます。
これを関数fの逆関数といいf-1と表します。
簡単に示すならば、三角関数sinπ/2=1に対して、逆三角関数sin-11=π/2ということです。
正確には、sinの逆三角関数y=sin-1xの定義域(xの変域)-1≦x≦1をセットにする必要があります。
三角関数sin・cos・tanの逆三角関数sin-1・cos-1・tan-1には特別に別名があります。
それぞれarcsin(アークサイン)・arccos(アークコサイン)・arctan(アークタンジェント)と呼ばれます。
sinπ/2=1における、π/2は半径が1の円の弧長を表します。逆関数sin-11=π/2はπ/2という弧長を表しているので、弧を表すarcが使われます。
さらに三角関数の逆関数は先に紹介した三角関数の逆数sec(セカント)・cosec(コセカント)・cot(コタンジェント)に対しても、それぞれarcsec(アークセカント)・arccosec(アークコセカント)・arccot(アークコタンジェント)と定義されます。
三角関数・逆三角関数 一覧
三角関数と逆三角関数を一覧にまとめてみましょう。
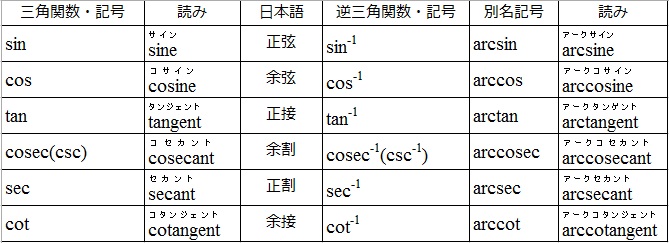
双曲線関数
三角関数は円x2+y2=1によって定義されるので、別名「円関数」とも呼ばれます。
双曲線x2-y2=1によって定義されるのが双曲線関数です。

sinhは双曲線正弦関数 (hyperbolic sine:ハイパボリックサイン)、coshは双曲線余弦関数 (hyperbolic cosine:ハイパボリックコサイン) と呼ばれます。
測量用の三角関数
天文学や航海術の測量で利用されるのが球面三角法です。
ここに特別に現れる三角関数があります。
![]()
versinは正矢関数、havは半正矢関数(haversine)、exsecは外正割関数(exterior secant)と呼ばれます。
三角関数のグラフ
上記で出てきたcosh双曲線余弦関数は身近な風景に隠れています。たとえば、垂れた電線やネックレスの描く曲線です。
このことから双曲線余弦関数のグラフは懸垂線と呼ばれます。

サイクロイド
サイクロイドとは、平面内において1直線上を円が滑ることなく転がるとき、円周上の定点が描く軌跡のことをいいます。
この仲間がいくつかあります。
アステロイド
アステロイドは、ある円内を、その4分の1の半径を持つ円が滑ることなく転がるとき、円周上の定点が描く軌跡です。
ヨハン・ベルヌーイ(1667-1748)やライプニッツ(1646-1716)らによって研究されました。
カージオイド
カージオイドは、ある円外を、それと等しい半径をもつ円が滑ることなく転がるとき、円周上の定点が描く軌跡です。

最新のグラフ描写ソフトを用いることで、曲面のグラフを見事に描き出すことができます。
方程式の風景からはとても想像できない、曲面の風景がコンピュータによって目の前に出現する様子に、ただただ驚かされます。


本連載で展開してきたように、三角関数のおかげでコンピューターの誕生に到る長い数学物語がありました。
そのコンピューターが三角関数のグラフを描く風景を眺めるとき、感慨無量の想いがします。
