
目次
正五角形の角度を解く
【問題】正五角形ABCDEの4つの角a、b、c、dを求めよ。
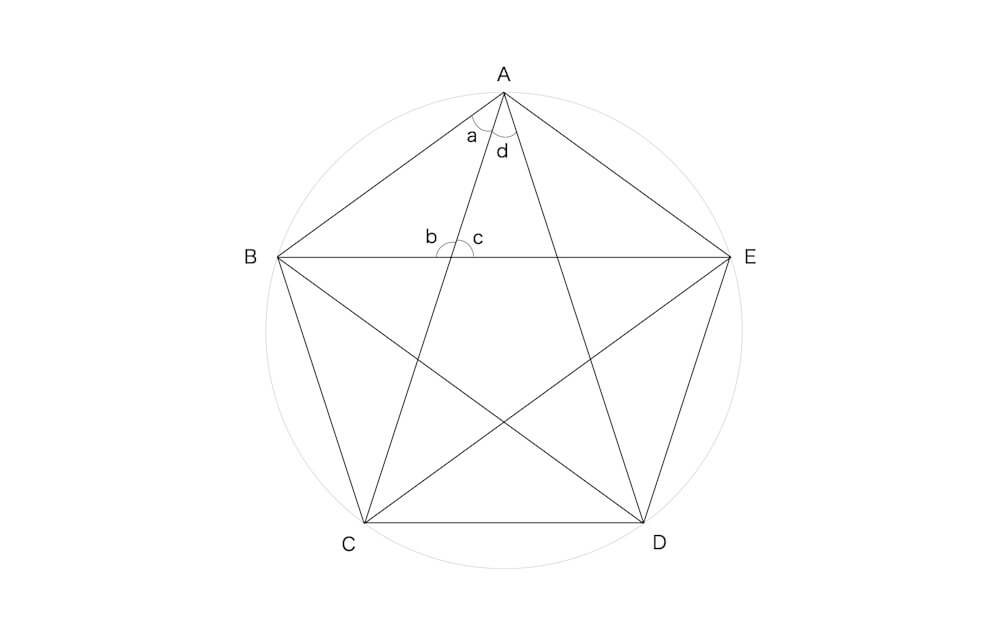
正五角形の内角はその和を五等分すればいい。正五角形は3個の三角形に分割される。三角形の内角の和は180°だから、正五角形の内角の和は180°×3=540°。
540°÷5=108°が正五角形の内角。すると、角bは内側の小さい正五角形の内角の反対側の角(対頂角)だから、b=108°。角cは角bの隣にあるから、c=180°− 108°=72°とわかる。
三角形ABCは二等辺三角形。角BACと角BCAが等しく、角ABCは正五角形の内角108°。だから、a=角BAC=角ACB=(180°− 108°)÷2=72°÷2=36°。三角形ACDも二等辺三角形。角ACDと角ADCが等しく、角ACD=c=72°だから、d=角CAD=180°−(72°+72°)=36°。
はたして正五角形ABCDEの対角線でできる角は36°、72°、108°のどれかになる。●1個が36°を表すとすると、●●、●●●はそれぞれ36°×2=72°、36°×3=108°を表す。
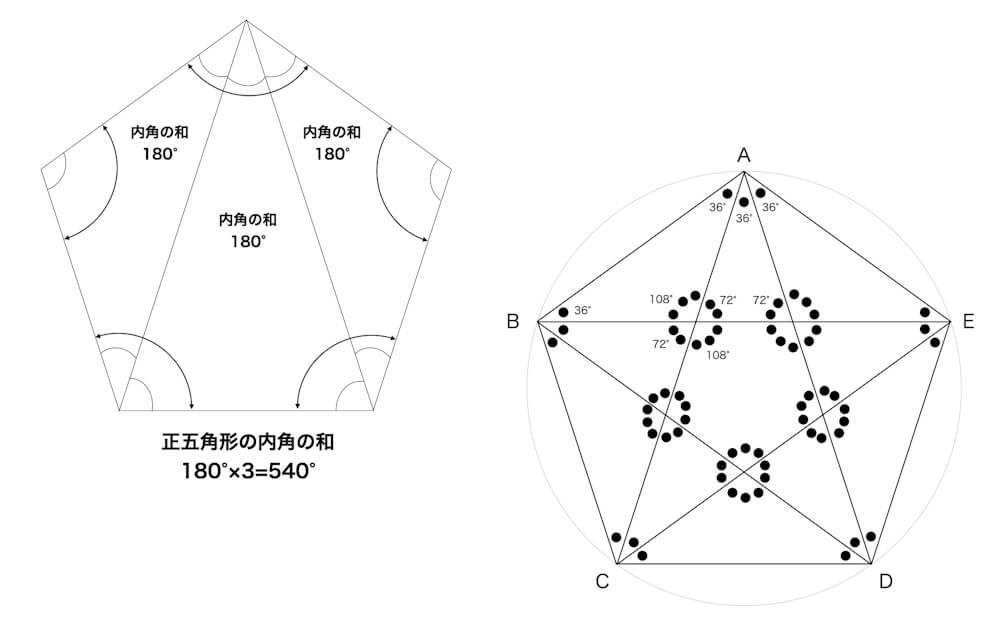
正五角形にある二等辺三角形と平行四辺形を探せ
【問題】内角が36°、72°、72°である二等辺三角形ACDと相似な二等辺三角形は? 正五角形の内部にある平行四辺形を探せ?
図のように二等辺三角形ACDと相似な二等辺三角形は2つある。向かい合う2辺がそれぞれ平行である四角形が平行四辺形。平行四辺形は向かい合う角もそれぞれ等しい。図で示した平行四辺形は向かい合う角は72°と108°。
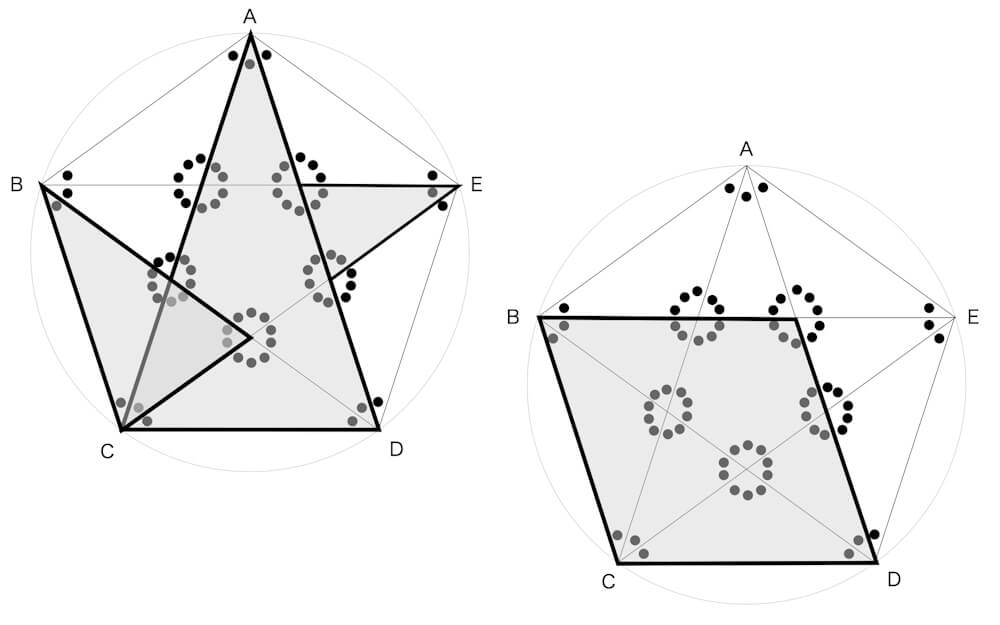
正五角形の線分比を解く
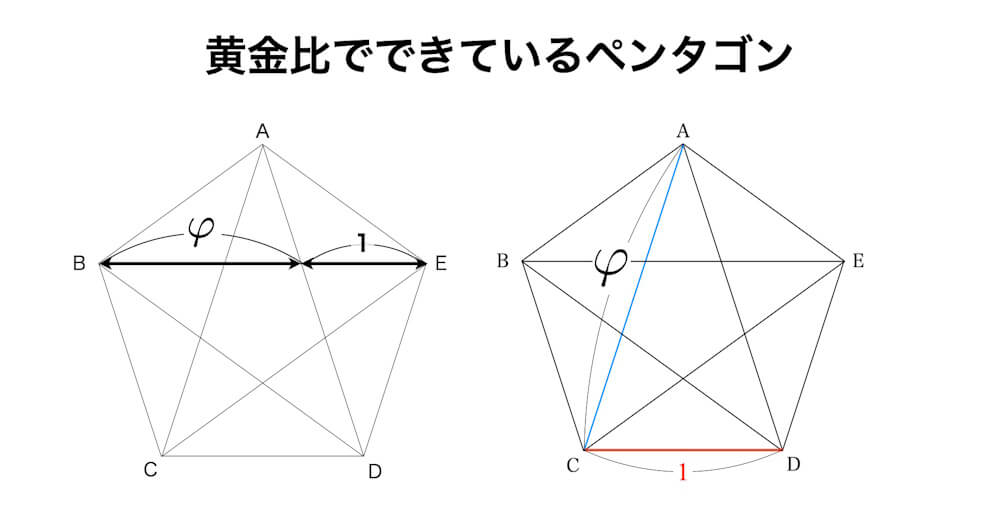
正五角形に含まれる2つの大きさが異なる二等辺三角形を利用して、正五角形の対角線の長さを求めることができる。正五角形の1辺の長さを1、対角線の長さをφとする。
図の青と赤の二等辺三角形は相似である。それぞれの辺の長さは、斜辺がφ:1、底辺が1:φ−1、となることがわかる。したがって、
φ:1 = 1:φ−1
が成り立つ。これより、
1×1 = φ×(φ−1)
φ²−φ−1 = 0
2次方程式の解の公式より、
φ = (1+√5)/2
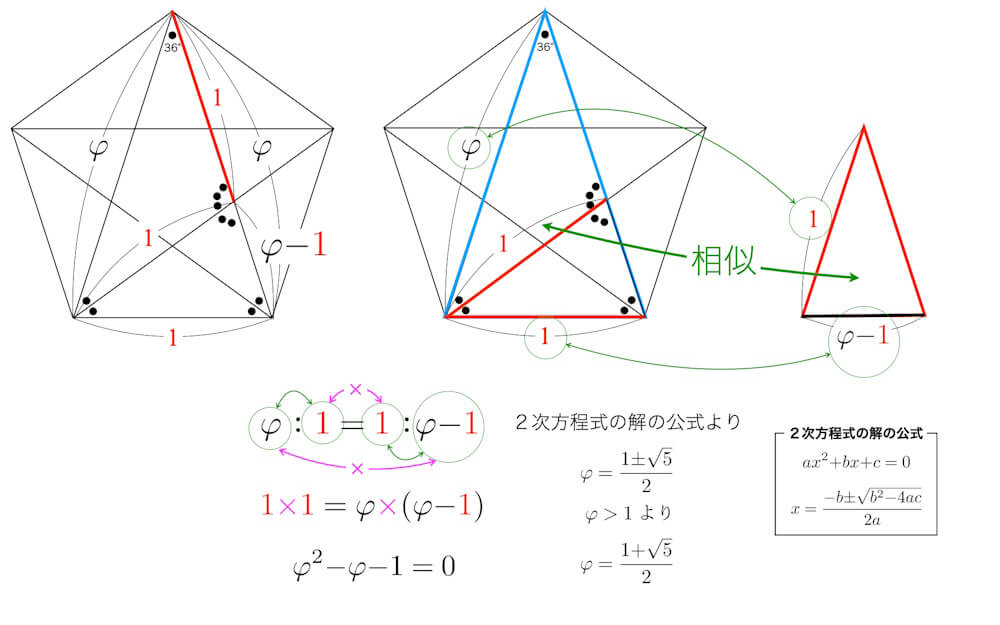
黄金比を計算する
こうして得られた正五角形の対角線の長さφを電卓で計算してみる。
「5」「√」「+」「1」「÷」「2」「=」
とキーを叩けば、1.61803398874が得られる。これが有名な黄金率φと黄金比1:φである。

正五角形は1辺:斜辺および、対角線の分割が黄金比であることがわかった。この性質を用いて定規とコンパスで正五角形を作図することができる。
正五角形を作図する
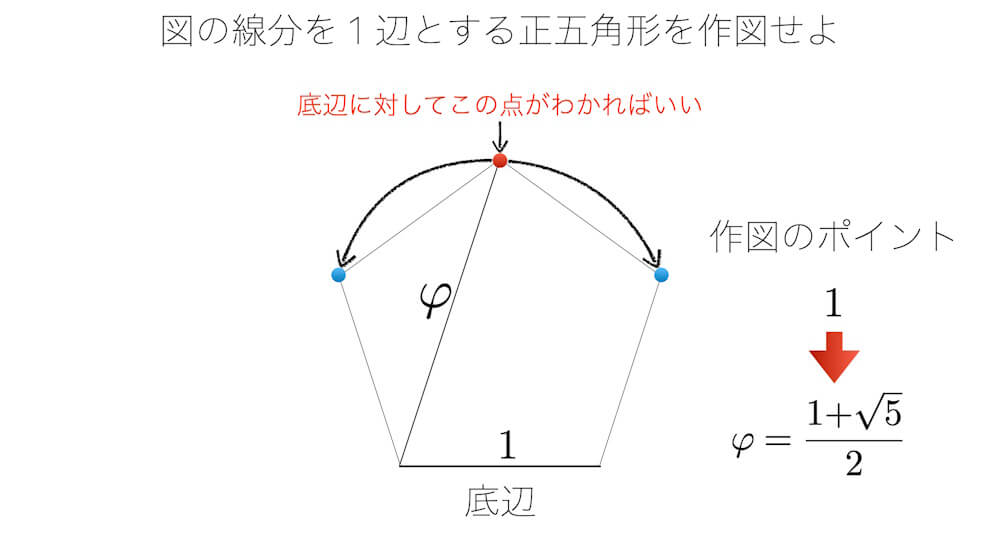
正五角形の1辺の長さを1とすると斜辺が黄金率φ=1.618…となることを用いて、正五角形を定規とコンパスで作図することができる。
次の図のように、底辺の真上にある頂点(赤点)が鍵である。この頂点がわかれば残りの2つの頂点(青点)がわかり、正五角形が完成する。
- ステップ1:一辺(底辺)ABを引く
図面の下部に描きたい正五角形の一辺を引く。その上部に正五角形が描かれることを考慮して一辺の長さと配置を決める。 - ステップ2:ABの垂直二等分線を引く
端点AとBを中心に円弧を描き、それらの交点を結んだ線分がABの垂直二等分線である。ABと垂直二等分線の交点をMとする。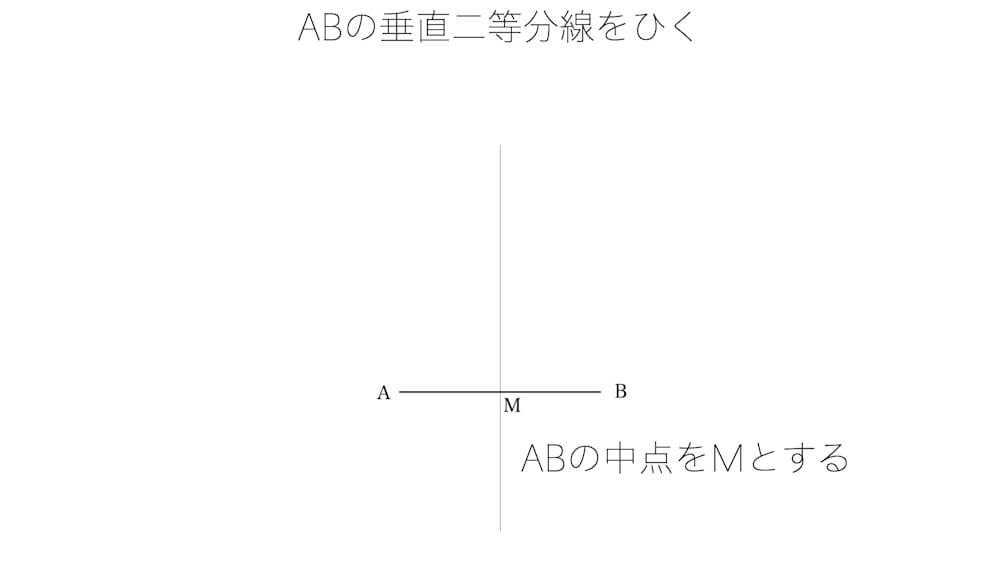
- ステップ3:MN=ABとなるNを垂直二等分線上にとる
コンパスでABの幅をとり、MN=ABとなるNを垂直二等分線上にとり、半直線ANを引く。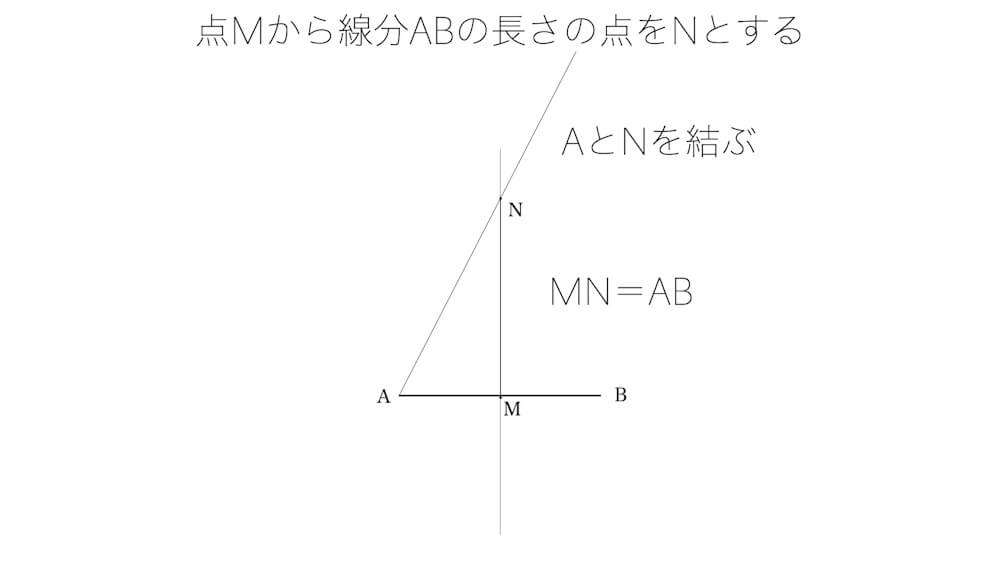
- ステップ4:NP=AMとなるPを直線AN上にとる
コンパスでAMの幅をとり、Nからその長さだけ進んだPをとる。すると、APがφ=√5/2+1/2となる。なぜなら、ANは三平方の定理で√5/2、NP=AM=1/2だから。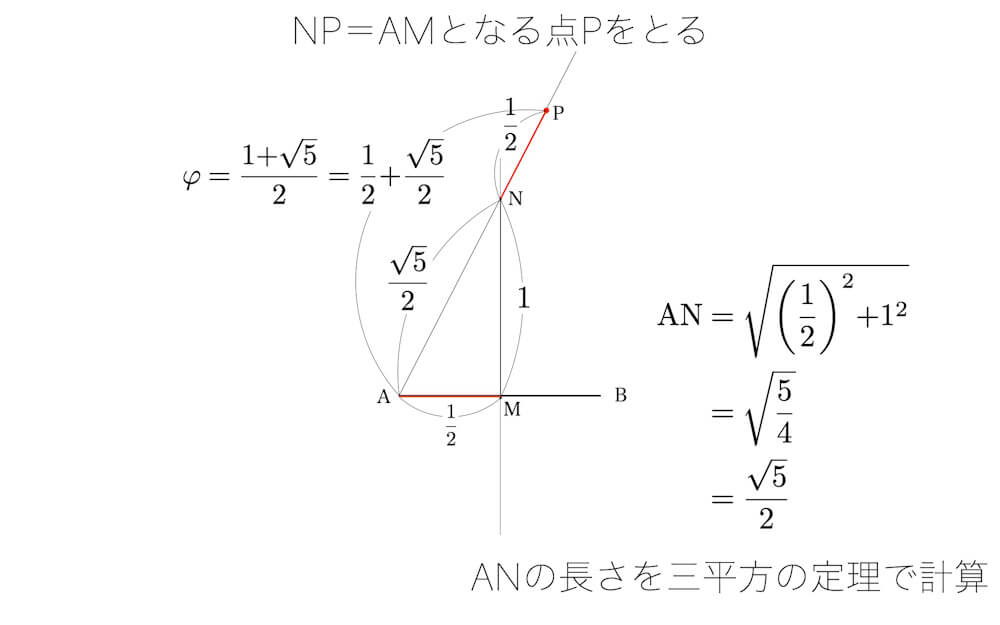
- ステップ5:半径APの円弧を描き、ABの垂直二等分線との交点をDとする
APがφなのでADがφとなるようにDをとれば、これが求める正五角形の頂点である。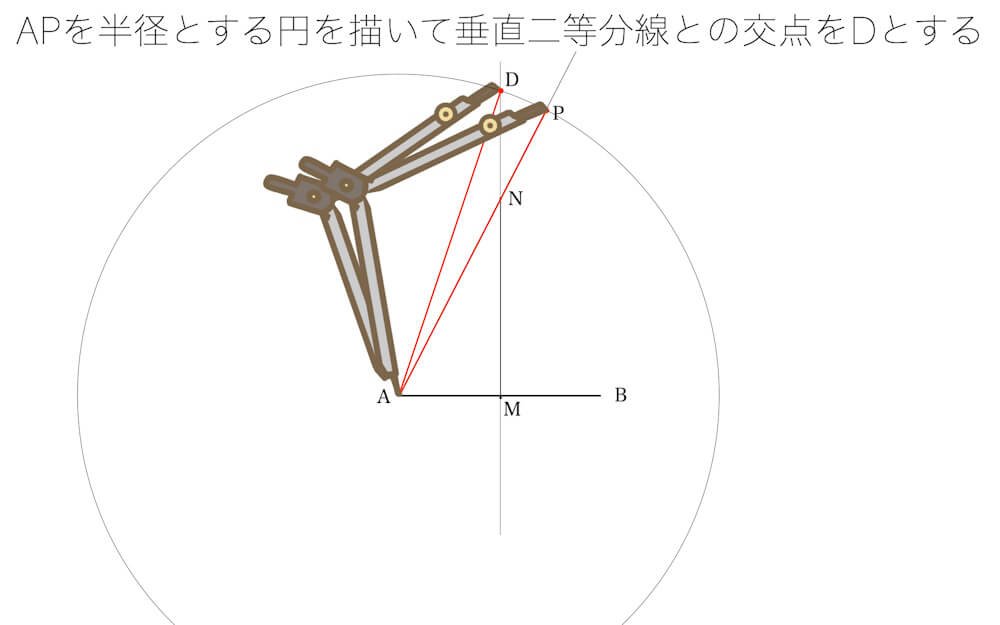
- ステップ6:残りの2つの頂点CとEを求める
コンパスでABの幅をとり、Dを中心に円弧を描く。AとBを中心に円弧を描く。2つの円弧の交点がそれぞれEとC。
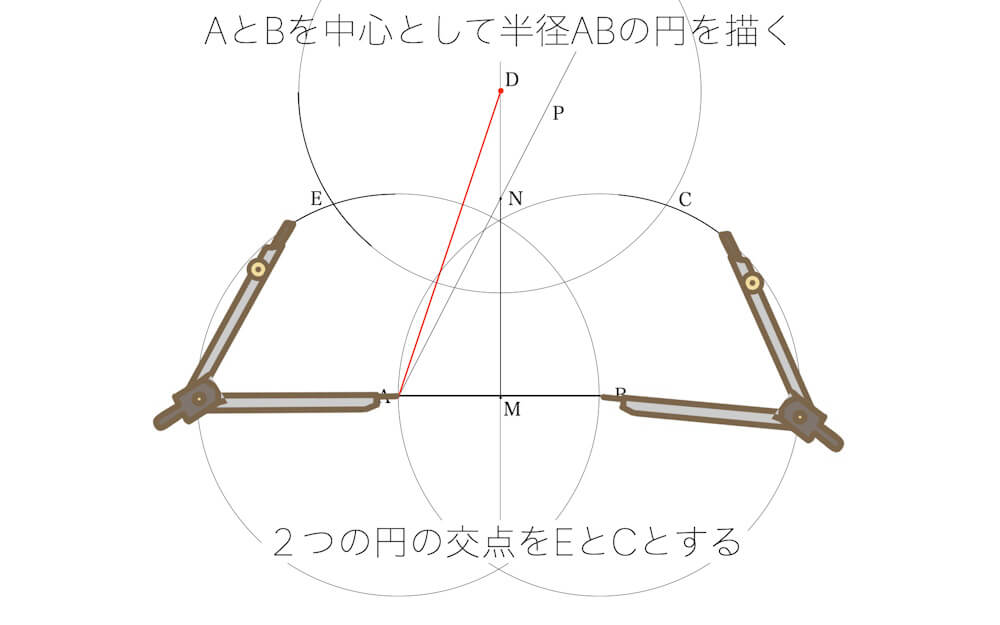
- ステップ7:BC、CD、DE、EAを結べば正五角形の完成
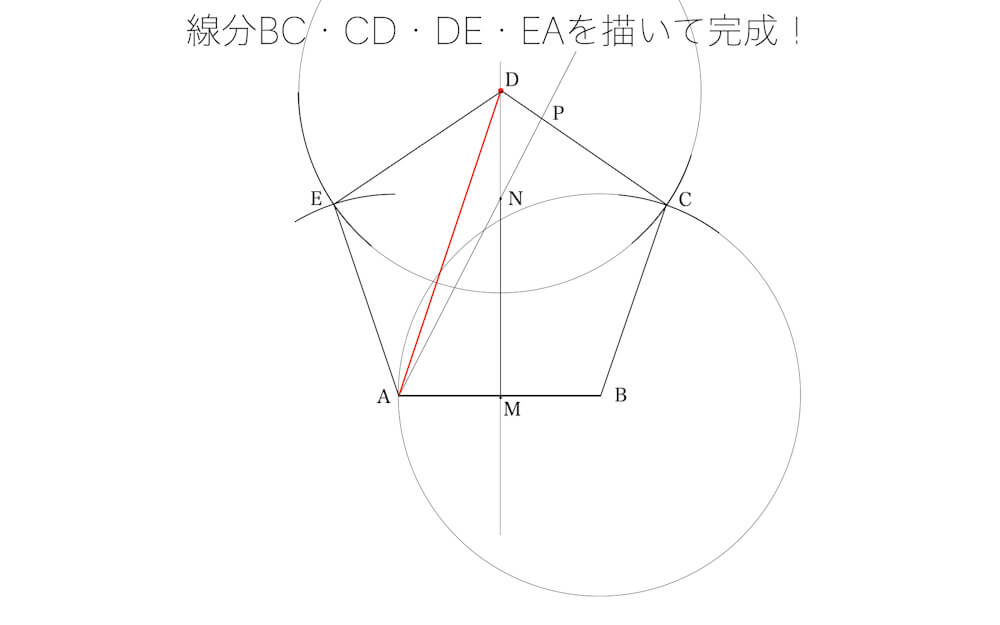
次回ペンタゴンの続きは、5角数とオイラーの5角数定理です。
インフォマティクスからのお知らせ
今回のコラムでは、美しい正五角形の作図を通じて、図形と比率の奥深さに触れていただけたのではないでしょうか。
このように図形を論理的に構築する力は、地理情報システム(GIS)の世界でも重要な役割を果たしています。
地図データの上にさまざまな情報を重ねて利用するGISソフトには、行政区画や建物形状などの情報を地図上で多角形(ポリゴン)として表現するための作図機能が備わっています。
インフォマティクスのGISソフト「SIS」(エスアイエス)は、以下をはじめ多彩な機能を備えています。
- ポイント、ライン、ポリゴンの作図・編集が直感的な操作で可能
- 行政区画や建物形状などのポリゴンを地図上に正確に描写
- 図形の形状や距離を用いた空間検索が可能
トライアルのお知らせ
📝無償版SISの機能紹介記事はこちら
GIS導入事例のご紹介
現場で求められるのは、直感的な操作性と高速な処理、精度の高い空間解析力。
インフォマティクスのGISは空間情報を扱う業務を支えるツールとして、行政、消防、インフラ、金融、教育・研究など幅広い分野で活用されています。
GISを活用して現場の課題がどのように解決されたのか、システムを導入されたお客様の事例をご紹介しています。
▼ GISのお客様事例はこちら
GISやAI機械学習を使った業務システムの構築に関するご相談を承っています。お気軽にお問い合わせください。
