目次
数学とは繋がりを探求する物語
三角関数sinは対数logを導き、そしてオイラーによるネイピア数eの発見と連載は続きました。物語はオイラーの手によってクライマックスへと突き進んでいきます。
π、sin、log、eのすべてが一本の数式に統合されていくことになろうとは、誰が予想したでしょう。
オイラーの公式とは
オイラーの公式とは、1740年頃にオイラーにより証明された等式です。
左辺はネイピア数 （自然対数を底とする複素指数関数）で、iは虚数、右辺のcos、sinは三角関数（正弦、余弦）を意味します。
すべてがつながるまでの後1歩｜虚数誕生物語
虚数i。
その不思議な名前の数なくして、π、sin、log、eのすべてが統合されることはありませんでした。
i×i=−1
という不思議な性質を持つ数です。
数の世界を「拡張」することで虚数は出現します。数と計算の関係から、数の世界が拡張されていきます。
「0」には二つの意味があります。最初に考えだされた0は「その位に何もない」という意味の「空位の0（数字の0）」で、古代バビロニアの人たちも使っていました。
ところが7世紀頃のインド人は「何もないものの個数」という意味の「無の0（数としての0）」を考案しました。そのおかげで、十進位取り記数法による数の計算ができるようになりました。
インドの数学者プラマグプタ（598-668）は著書の中で「数としての0」のルール── a+0=a、0+0=0、a-0=a、0-0=0、a×0=0、0×0=0など──を説明しています。
数0を黒点「・」で表したインド数字は8世紀頃にアラビアに伝わり、そこから12世紀頃ヨーロッパに伝わり、16世紀に現在の数字であるアラビア数字になりました。アラビア数字は計算に適した数字であることからアラビア算用数字とも呼ばれます。
こうして、数0ができあがることで「負の数」が現れます。たし算3+□=0を満たす□が-3という負の数です。自然数（1、2、3、…）と0と負の自然数を合わせた数が「整数」です。
この□を用いた式は方程式に他なりません。自然数と0だけの数の世界とたし算（ひき算）を考えたときに「負の数」が必要となると考えるのです。
同じようにして整数とかけ算を考えることで分数（有理数）という新しい数が必要となります。3×□=−5を満たす□は、整数の世界には見つかりません。
□=−5/3という数が有理数です。ちなみに、この用語は英語rational numberの訳なのですが、ratioとは比を意味するので直訳は「比なる数」という意味です。この奇妙な翻訳のいきさつはまた別の機会で述べることにします。
有理数とかけ算を考えることで新しい数が必要になります。□×□=2を満たす□は、有理数（自然数、整数を含む）の中に見つかりません。
□=1.41421356…は無理数（irrational number）と呼ばれる数です。√2とも表される数で、小数点以下が循環することなく無限に続く数です。自然数、整数、有理数、無理数をまとめた数の世界が「実数（real number）」です。
普通私たちが使う数は実数です。黄金比φ（1.618…）、円周率π（3.14…）、ネイピア数e（2.718…）も実数です。
数と計算は文明とともに進化してきました。その歴史の中で、数は自然数、0、負の数、有理数、無理数、実数と、大きく拡張されていきました。
そして問題の拡張に遭遇します。方程式□×□=2は実数の中に□が見つかりますが、□×□=-2という問題です。
この方程式を満たす□という数は実数の世界には存在しません。そこで登場するのが、虚数です。
虚数i
この新しい数「虚数」が発見され認められるまで実に長い年月を要しました。
そもそも0や負の数という実数でさえ、長い時間を経てようやく普及したのですから、虚数が人間の中でリアリティを獲得するのに長い時間がかかるのは当然です。
16世紀、イタリアの数学者カルダノ（1501-1576）は、3次方程式の解く際にはじめて虚数の概念を導入しました。
フランスの哲学者・数学者デカルト（1596-1650）が虚数を「想像上の数」と名付けたことが英語のimaginary numberの語源となりました。
デカルトによるこの命名は、新しい数を否定的に捉えていたからでした。デカルトの時代、0や負の数ですら架空の数と考えられていました。
□×□=-2を満たす数を数学者ですら容易に受け入れることはできませんでした。面白いことに、現在わが国の理工系学生でさえ、虚数は「実在しない数」だと思っている人が大勢います。
その原因は、実数にはあるリアリティ（例えば、定規にかかれた数字は実数を表す）が虚数にはないからだと考えられます。
さらにそのことが「虚数」や「imaginary number」という否定的な言葉によって後押しされているのではないでしょうか。まさにデカルトのネガティブ思考は現代にも生きています。
虚数は実在します。数の世界に実在します。
実数も同じで、数の世界に実数は存在します。実数も虚数もどちらも人間が考え出した“imaginary”numberだということです。
ところで、数の拡張はどこまでいくのでしょうか。
虚数iと2つの実数xとyを合わせた、複合的な（complex）数x+iyを複素数（complex number）と呼びます。これは2元数とも呼ばれます。2次元の数という意味です。
興味深いことに、3元数（3次元の数）は“役に立たない（論理的整合性を持たないという意味）”数なのですが、4元数（4次元の数）は“役に立つ”数です。
発見者にちなんでハミルトン数とも呼ばれます。コンピュータ・グラフィックスの世界では、3次元の回転を計算するのに4元数が応用されています。
このような数の世界の拡張に関する分野を「超複素数理論」といいます。超複素数理論は驚くべき定理を私たちに突きつけてくることになるのですが、話を元に戻しましょう。
そして、すべてがつながる
かくして、数の主人公
π、sin、log、e、そしてi
はすべて揃い、驚異の風景を描く準備ができました。
1748年、オイラーは著書『無限解析序説』の中で、その風景を淡々と描いていきます。タイトルにある無限∞も加えてすべてが繋がる風景が描き出されていきます。
π、sin、log、e、i、そして∞
こちらの記事で紹介しましたが、logの考案者ジョン・ネイピアの原書に、私は京都大学で遭遇しました。
同じ本棚に『無限解析序説』の原書もあり、手にとることができました。その「第7章 指数と対数の級数表示」と「第8章 円から生じる超越量」が今回の舞台です。
オイラーの『無限解析序説』（京都大学数学教室所蔵）
こちらの記事で、ネイピア数eが次のように表されることを紹介しました。
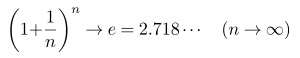現代の教科書にはこう書かれます。
第7章では、この詳細が述べられていきます。ここから先はオイラーの記法にできるだけ従って見ていきます。その方がある意味簡潔で分かりやすいからです。
ただし、文字の使い方のいくつかは分かりやすいものに代えていきます。オイラーは、iを虚数ではなく無限大（∞）として用いています。無限（infinity）の頭文字と考えられます。
オイラーは虚数を√-1として使っていますが、実はこれは現在でも使われている表し方です。もちろんiも一般的に使われますが、電気工学で虚数を使う際には、電流をIと表すので、虚数はiではなくjが使われます。
オイラーがi（無限大）としているのを∞に置き換えていきます。すると、ネイピア数eは次のように表されます。
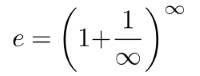実際、∞部分を“大きな数”として10000として計算してみると
となり、e=2.718281828…の近似値を表すことがわかります。これはコンピュータだから計算できたことで、18世紀にこの計算は容易ではありませんでした。
では、オイラーはいかにしてこの結論に到達したのかを追ってみましょう。
オイラーの出発の式（ωは無限小）
オイラーは次の計算から出発しました。
オイラーの出発の式（ωは無限小）
なぜ、このような形をオイラーは考えたのでしょうか。
オイラーの次の記述がヒントを与えてくれます。「たとえば、次の数の対数を求めてみよう」
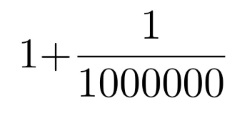と述べています。この数は、これまでの連載に何度も登場した、ネイピアの自然対数の底
を連想させます。ωが無限小を表します。
オイラーは、ニュートンの二項定理を用いて、右辺を展開していきます。そして、右辺の指数部分∞を有限な形に変形することで、次を得ました。
さらにこの式で、z=1とすれば次が得られます。
いよいよ、eが現れる瞬間です。オイラーは、この式でk=1としたaをeを用いて表すことにすると記しています。
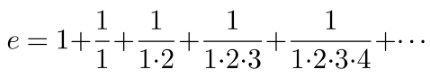そしてこの式からeは容易に算出されます。これだけを計算してみても、2.70…と計算されます。オイラーは多くの項のたし算を行い、
e=2.71828182845904523536028
と算出し、「一番最後の数字もまた正しい」と述べています。確かに正しい数値は
e=2.7182818284590452353602874…
ですから、オイラーの言うとおりです。
さて、このeを用いると、これまでに現れた式はeを用いて表されることになります。
第7章の結論
これが、ネイピア数eと指数関数、誕生の瞬間です。
これより、前回のコラムでネイピア数の「0.9999999の謎解き」の謎が明らかになります。
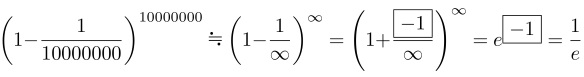ネイピアの対数の謎解き
第7章 指数と対数の級数表示 冒頭部分
オイラーの計算の旅もあと少しでフィナーレを迎えます。
第8章 円から生じる超越量、その冒頭でオイラーは、半径が1の円周の半周は
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446…
であると述べ、「表記を簡単にするために、これを
π
と書くことにしよう」と述べています。
私たちが慣れ親しんでいる記号「π」誕生の瞬間です。ちなみに、上記の円周率の数値はすべて正しい！
オイラーは三角関数の関係を述べていきます。それは現在の高校数学の教科書に書かれてある公式です。中でも次の公式は、最も基本的なsinとcosの関係式です。
三角関数の基本公式
オイラーは、これを虚数iを用いて因数分解します。
ここから、次の関係式を導き出していきます。
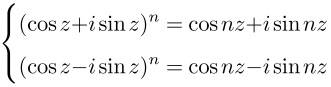
ド・モアブルの公式（nは自然数）
これは、現在ではド・モアブルの公式と呼ばれているものです。
この2式の辺々をたし算、ひき算してそれぞれ2、2iで割ることで、次のcosとsinの式が得られます。
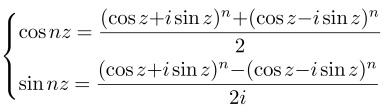さて、nを無限大（∞）、zを無限小として、nz=x（xは有限値）とすると
なので（極限の書き方をしないオイラー流の書き方）、上の式に代入すると、
ここで、第7章の結論を思い出します。
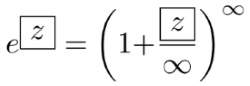
第7章の結論
これより、cos xとsin xがeを用いて表されます。
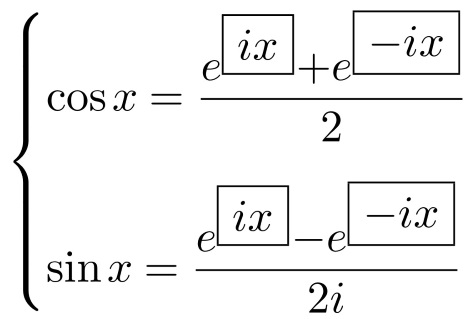
この2式から次が導かれます。
オイラーの公式
ついに到達しました。これが、今から268年前、オイラーが辿った軌跡です。
オイラーの公式を鑑賞する
- オイラーの公式
- 作者：オイラー（1707-1783）
- 完成年：1748年
すべてのはじまりは三角比sinです。ネイピアはsinの天文学的計算を楽にするために対数logを作り出しました。
そして、オイラーによって、eが発見され、ついには虚数と∞の仲立ちによってそれらすべてが結びつくという驚異の数式です。
- オイラーの公式のxにπを代入した式
- 作者：オイラー（1707-1783）？
- 完成年：1748年？
そしてオイラーは虚数にリアリティを与える決定的な演出をしてみせるのです。xにはすべての実数が代入できるので、オイラーはとっておきの実数πをxに代入します。
右辺はcos π＝-1、sin π＝0となるので、最初のオイラーの公式は一変します。もはや関数sinやcosの姿は消えて、数だけの関係が現れてきました。
虚数iは突然「i×i=-1」という性質を持つ数だといわれても、にわかに信じがたく感じます。実際、数学者自身がそうでした。
この関係式は、虚数iにビビッドな印象を与えてくれます。3つの実数eとπと-1に囲まれたおかげで、虚数i自信が自らの実在性に自信をもてることになったのです。
実際、オイラーは虚数が持つ絶大なる威力を見いだし、新しい数学を切り開いてみせました。
- オイラーの公式のxにπを代入した式の右辺を0にした式
- 作者：オイラー（1707-1783）？
- 完成年：1748年？
0を使った演出。左辺を計算した結果が0になるとは！
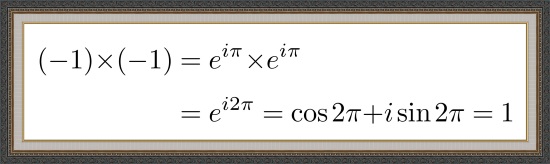
- オイラーの公式を用いた(-1)×(-1)=1の証明
- デザイン：桜井進（1968-）
- 制作年：2016年
マイナス×マイナスがなぜプラスになるかを、ネイピア数、虚数、三角関数らが教えてくれます。
- 「虚数の虚数乗が実数になるなんて！」オイラーを驚嘆させた絵
- 作者：オイラー
- 出典：Euler, Opera Omnia, Ser.1,Vol.6
「虚数の虚数乗が実数になるなんて！」とオイラーを驚嘆させた絵。
数学は至極の芸術である
土にさわってるうちに、自然に形がうまれるくるんや。こんな形にしよか、あんな色にしよか、ってなこと頭で考えてんのとはちがうんや。自然にうまれてくるのを待つのや。
なあ、けど、その自然がなかなか難しい…。あのなあ、こんなええもんつくりたいとか、人に褒められようとか、アホなこと考えてるうちはろくなもんでけんわ。
つくるでない、掘り出すのや。土の中に、美しいもんがいてな、だしてくれ、はよだしてくれ、ゆうて泣いてんね
出典：映画「男はつらいよ 寅次郎あじさいの恋」
山田洋次監督、映画「男はつらいよ 寅次郎あじさいの恋」（第29作）、片岡仁左衛門扮する人間国宝陶芸家、加納作次郎が京都の料亭で寅さんに涙ながらに語るシーンです。
私たちは五感を通して音や色の調和を感じとることができます。それが音楽や美術といった芸術を創り上げます。
オイラーの公式はオイラーが作ったのではありません。
出自が異なるsin、log、ネイピア数e、円周率πたちが、実は深いところ（虚数の世界）で結びついていることをオイラーは発見したのです。
数の世界にも本来あるべき「自然」が存在し、音や色に調和があるように数にも「調和」があることをオイラーは教えてくれます。
オイラーやネイピアは、私たち人間には数の調和を感じ取ることができる特別な感覚があることを証明してくれたといえるでしょう。
そこから数学という芸術が創られていくのです。
三角関数の物語はつづく
オイラーの公式を振り返るとき、すべてはsinにはじまりsinに終わることがわかります。
1748年の『無限解析序説』において、オイラーは関数概念の概念規定を試みています。数学史上初めてのことです。
ネイピアは20年かけた対数表作成の計算によって、実数を実感したと思われます。その結果、小数点「・」が発明されました。ネイピアの中では、対数“関数”の感覚が生まれていたのではないでしょうか。
その130年後、オイラーの中から「関数」が形になり始めました。60進法の角度の誕生まで遡るならば、三角比が三角関数に変身するのに実に四千年ほどかかったことになります。
『無限解析序説』の表紙裏の挿絵に「TABLE DES SINUS」（三角関数表）を見つけることができます。
オイラーの数学が三角関数とともにあることを、これからも見ていきます。
いよいよ始まったオイラー物語をお楽しみに。
オイラー著『無限解析序説』（1748年）表紙裏の挿絵
