平面幾何｜重心【東京都の重心はどこ？】

重心の重は重力の重

数学の重心の話に入る前に、まずは物理学の重力から始めましょう。

重力とは何か

重力（gravity）とは「重さ」のことを指します。

地上の物体に重さ（重力）があるのは、小さな物体と大きな地球との間に万有引力と呼ばれる力が働いているためです。ニュートンの万有引力の法則によると、2つの物体の間に働く力は、それぞれの質量の積に比例し、距離の2乗に反比例します。

地球に比べて月の質量と半径はともに小さく、質量は地球の約81分の1、半径は約4分の1です。そのため、月の上では同じ質量の物体に対する重さ（重力）は、地球上よりも小さくなります。

1/81×4×4＝0.197…（正確には0.165…≒1/6）

これが、月での重さ（重力）は地球の約6分の1になるといわれる理由です。

さて、地上のすべての物体には地球の中心方向に重力が働きます。地球は大きいため、この重力の方向はほぼ平行で、ほとんど同じ向きに働いていると考えることができます。

重心（center of gravity）とは重さの中心

シーソーに乗ったときのことを思い出してみましょう。

同じ体重の人が両端に乗った場合、中央で支えられた長い台は水平に保たれたまま動きは止まります。異なる体重の人が乗った場合には重い人の端が下方向に、軽い人の端は上方向に支点に対して回転します。

もし支点をずらすことができれば、支点を中央から重い人の方にずらすことで回転を止めて台を水平にすることができます。左右の「人の重さ×腕の長さ（支点から人までの長さ）」が等しくなるように支点を調節すれば、台は水平になることを理科で習います。

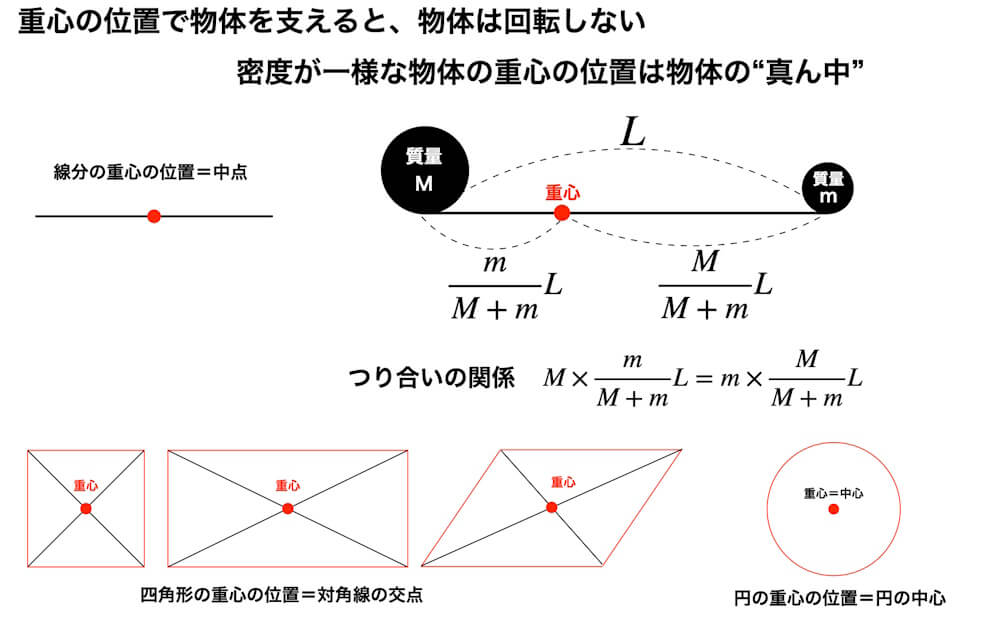
これが"つり合う"ということです。シーソー台がつり合う支点の位置が重心です。重心で物体を支えるとその物体は回転しません。物体をその1点のみで支えることができる点という意味で、重さの中心すなわち重心（center of gravity）と呼ばれます。

重心の位置

重心の位置は形状により異なります。

• 線分：中点
• 四角形（正方形・長方形・平行四辺形など）：対角線の交点
• 円：中心

シーソーのつり合いの関係「人の重さ×腕の長さ（支点から人までの長さ）」が等しいを定式化すれば、次のようになります。

重心の位置＝腕の両端の質量の逆比に腕の長さを内分した点　…（☆）

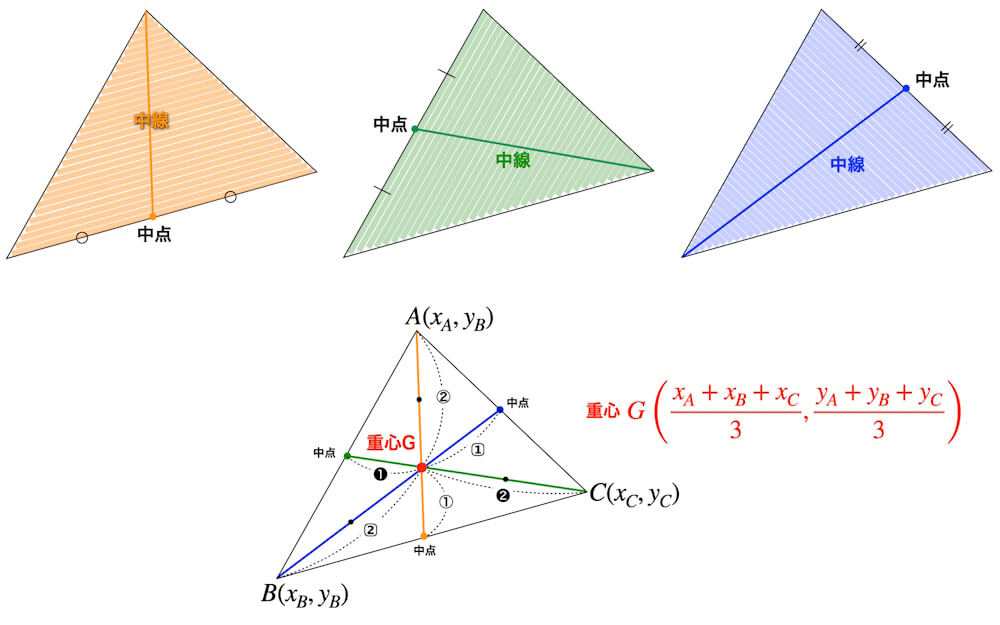
三角形の重心

三角形の重心は中線の交点です。中線とは、三角形の頂点から対辺の中点を結ぶ線分のことです。

点Aから辺BCの中点を結んだ中線、点Bから辺ACの中点を結んだ中線、そして点Cから辺ABの中点を結んだ中線、これら3つの中線は1点で交わります。この点が三角形の重心です。この重心で三角形の板を支えれば、つり合うということです。三角形コマの心棒の位置は重心とすれば、うまく回ります。

三角形の板が細かい棒でできていると考えます。それぞれの棒の重心（中点）を結んだ直線（中線）上に三角形の重心はあるはずです。はたして、三角形の3つの中線は交わり、この交点が三角形の重心となります。

三角形を座標平面上で考えると三角形の重心の座標はx座標、y座標はそれぞれ3頂点のx座標、y座標の相加平均（3つの和の3分の1）で与えられます。

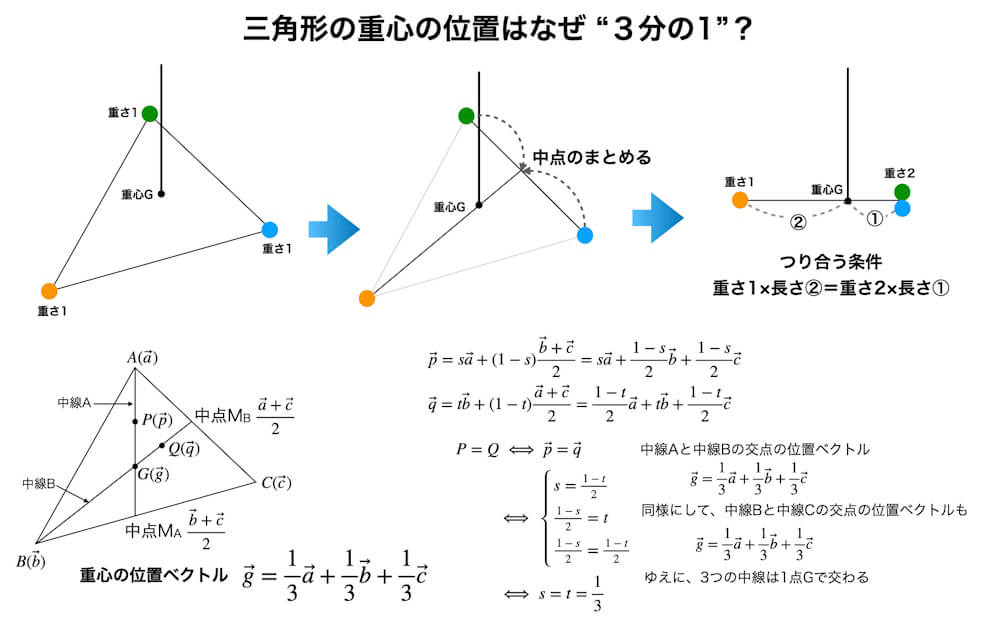
三角形の重心の位置はなぜ“3分の1”なのか

一番分かりやすい考え方は、シーソーのつり合いで考える方法です。

三角形の板全体ではなく、3頂点に質量が偏っているとします。どの重りも重さが1だとします。図の緑と青の重りは、その中点に合わせて重さ2の重りがあるようにできます。

オレンジと、この合わせた重りを結ぶ線分においてつり合いの位置を考えると、公式（☆）より、オレンジの重りから重心までの長さが2で重心から重さ2までの長さが1となります。すなわち、三角形の重心は中線を2:1に内分する点です。

ベクトルの方法で計算することもできます。3頂点の位置ベクトルを用いて、中線上の点の位置ベクトルを表すことで、パラメーターの連立方程式を解くことに帰着します。はたして、パラメーターの値が3分の1であることが示されます。

重心の簡単な見つけ方

次のような形の重心は、重力を使うことで簡単に見つけることができます。ヒントは三角形の場合と同じように、重心がある2本の線（垂線）を求めることです。その2本の線の交点が重心です。

重心を見つける手順

1. 問題の形を紙の上に描いて切り抜きます。
2. 切り抜いた紙のどこでもいいので虫ピンを刺してぶら下げます。
3. つり合ったところでピンから垂線を紙に描きます。
4. 今度は別の位置に虫ピンを刺してぶら下げます。
5. 同じようにつり合ったところで、ピンから垂直な線を紙に描きます。

この2本の線の交点が重心です。

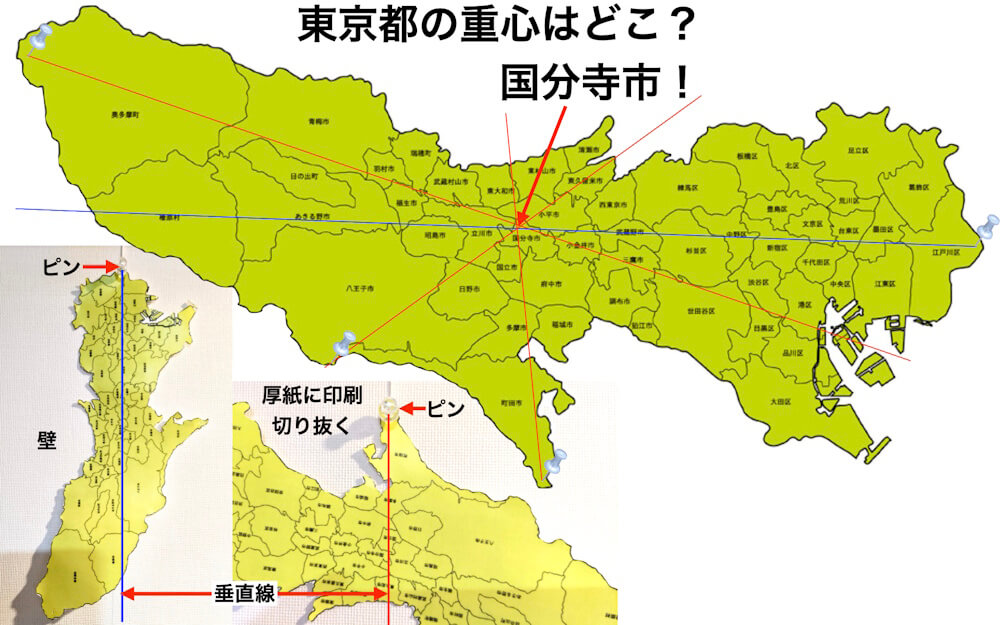
実際には、写真を撮って画像データ上に垂線を引く方法が効率的です。パソコンの画面上で重心を求めることができます。

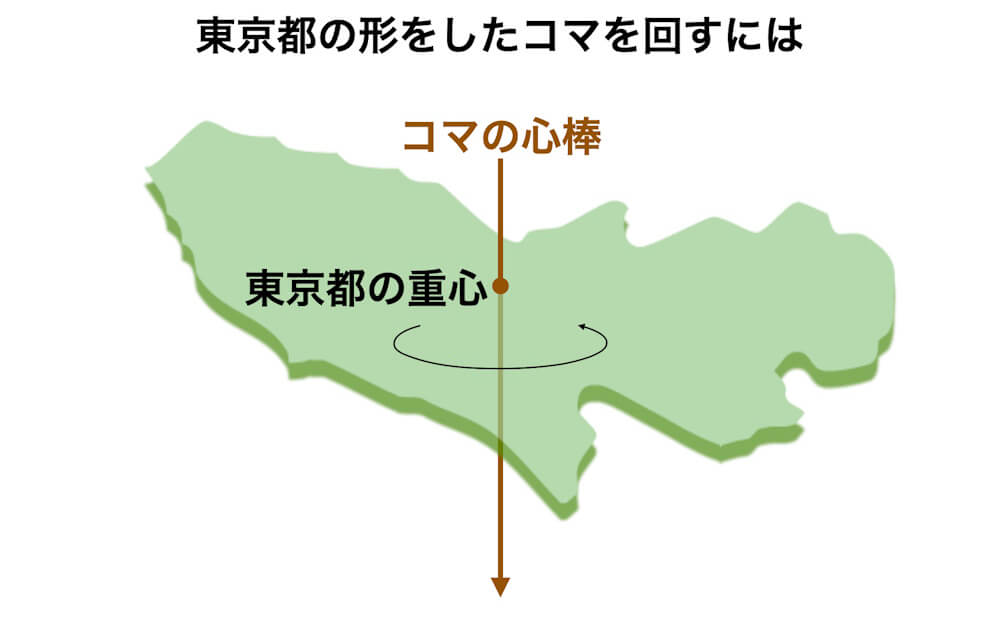
東京都の重心の位置はどこ？

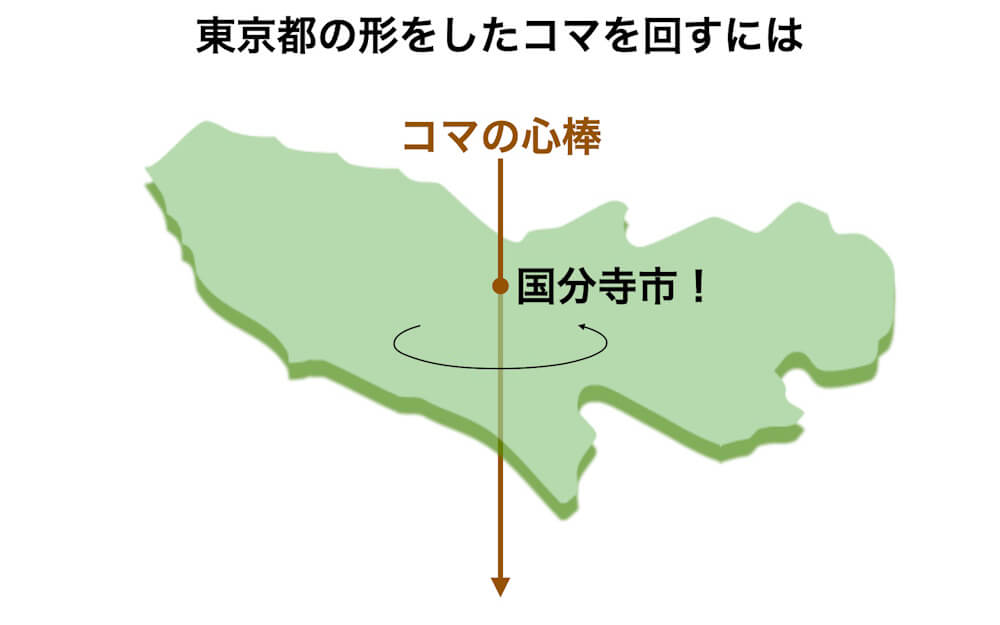
これと同じ方法で東京都の地図の重心を探してみると、国分寺市が重心の位置であることがわかりました。検索してみると、国分寺市の公式ホームページに国分寺市が東京の重心だと載っていました。

地図と重力の関係｜ジオイド

東京都の地図が登場したところで、地図と重力の“深い”関係について説明しましょう。

山の高さを表すときに使われる「標高」とは、海面からの高さ（海抜）のことです。水は高い所から低い所へ流れますが、実は平らに見える地面でも、水が流れる所があります。これは、重力が地下の密度構造の違いにより変化するためです。重力の分布が異なると、平らに見える地面でも水は流れるのです。

平らに見える地面でも、密度が相対的に大きい物質が地下深くに存在していると、その真上に周辺から水が引き寄せられ流れてきます。これは、密度が相対的に大きい物質が地下にある地点は高さが低く、その周辺では高さが高いことを意味します。

この状況を次のように表します。
地球を仮想的に表した楕円体から測って、密度が相対的に大きい物質が地下にある地点では「標高の基準となる高さ」が高くなり、周辺部では「標高の基準となる高さ」が低くなるとします。

衛星測位で決まる、ある地点の地球を仮想的に表した楕円体から測る高さを「楕円体高」と呼びます。このとき、「標高」「標高の基準となる高さ」「楕円体高」の関係は次の式で表されます。

標高　＝　楕円体高　−　標高の基準となる高さ

平らに見える地面とは「楕円体高」が等しいことを意味します。

たとえば、地下に密度の大きい物質がある地点の「楕円体高」と「標高の基準となる高さ」がそれぞれ10mと4m、その周辺箇所では10mと1mであるとします。

すると、どちらの地点も「楕円体高」は10mで等しいですが、標高は前者が10m−4m＝6m、後者が10m−1m＝9mとなり、地下に密度の大きい物質がある地点のほうが標高は低くなります。

このように、平らに見える地面（「楕円体高」が等しい）でも、重力の分布が異なる（「標高の基準となる高さ」が異なる）と水が流れることを説明できます。

この「標高の基準となる高さ」にあたるのがジオイド高です。地上の位置を測るためには、重力の正確な測定が重要になります。国土地理院では、正確な地図作りのため、重力の精密な測定に取り組んでいます。

本コラムで扱った重力の分布や標高、ジオイド高は、都市計画や社会インフラ整備、津波・洪水による被害軽減に役立つ重要な情報です。

空間情報クラブでは、標高や災害対策・防災に関するコラムを多数公開しています。ぜひご覧ください。

また、弊社のGISソフト「SIS」には無料版もあり、各種データを読み込んで操作をお試しいただけます。この機会に、GISで作図や検索、空間分析、3D表示などを体験してみませんか？

＜参考＞国分寺市ウェブサイト、国土地理院ウェブサイト