目次
微分積分とは
数学の威力はその汎用性にあります。
たとえば
- 湯飲み茶碗のお茶やお風呂の温度
- 薬の吸収
- マルサスの人口論
- ラジウム(放射性元素)の半減期
- うわさの伝播
- アルコールの吸収
- 事故危険率
- 水中で吸収される光量
- 肉まんの温度
これらの異なるすべての現象を同じ数式で説明できる──それが微分積分です。
微分とは刻々と変化する運動の様子──瞬間(微かな時間)を定量化する手法であり、積分とは刻々の変化を合計(積算)する手法です。
微分では変化の速さを求めることができ、積分ではその変化を積み上げて全体量を求めることができるわけです。

微分積分=小石?
大昔、数字がまだ存在していなかった時代、私たちが飼っている動物を数えるのに用いた道具が小石でした。
小石を意味するラテン語がcalc(カルク)。calcium(カルシウム)のcalcです。calc=計算の由来です。
calculateは「計算する」、calculatorは「計算機」、pocket calculatorは「電卓」です。そして、calculus。元々は「計算法」を意味するこの言葉には「微分積分学」の意味もあります。
微分法と積分法はまさに計算法です。それも曲者である“曲”を計ることができる最強の計算技術が微分積分学──calculusなのです。
人類が「曲=運動」をいかに理解しようとしてきたのかを振り返っていきます。
アリストテレスの運動論
そもそも「運動とは何か」という問題が発端です。
何が運動を起こさせる原因なのか、運動する先にどんな未来があるのかという運動の過去と未来を語るため、古代ギリシャ時代から運動それ自体の本質が研究されてきました。
アリストテレス(前384-前322)は身の回りの運動を注意深く観察することで、力と運動の関係を考察しました。物の本性は静止であり、運動している物体には絶えず力が働いているという結論を得ます。
アリストテレスはまた運動を2つに分類しました。力が物体に内在するために自然に生じる運動(自然運動)と、他から力が加わって生じる運動(強制運動)です。
自然運動の代表例が物の自由落下運動です。物が下へ落ちる理由をアリストテレスは次のように説明しました。
物が自分にとっての“自然な”場所である地球の中心に落ち着こうとする運動が自由落下運動であり、あたかも家にたどり着こうとする人の足取りが自分の家に近づくにつれて速くなるように、物もまた“自然な”場所に近づくほど速くなるのが加速する理由である、と。
それに対して、投げられた物の放物運動は、手から物に力を加えられる強制運動になるといいます。すると、手から離れた後、物にはいったいどんな力が働いているのかが問題になります。
物に接触するのは空気しかないと考えたアリストテレスは、「自然は真空を嫌う」とすれば、物が手から離れた後に生じる真空部分を嫌い、その部分に空気が入り込んでくることでその空気が物を押し続けると説明をしました。
今からすればおかしな考え方ですが、運動の本質を合理的に説明しようとした精神こそ画期的だったといえます。
その証拠に、アリストテレス後の天文学者ヒッパルコス(前190ごろ-前120ごろ)が三角関数表を作り始め天体の運動を説明してみせました。
コペルニクスの地動説とガリレオの慣性の法則
14世紀のヨーロッパでは大砲が使われ、弾道理論が求められていました。
打ち出された弾丸はアリストテレスが言うように空気に押されているのではなく、空気が抵抗になって運動していると考えられるようになりました。
当時の科学者は、弾丸に加えられた力が弾丸を推進させるために運動(放物運動)が持続すると考えたのです。
自由落下運動については、物体の重さが物体自身に働く力となり、落下中にその力が蓄積していくことで物体に働く力が増えていく、すなわち加速が生じると考えました。
こうして「慣性」すなわち力を受けなければ物体が等速度で運動状態を保持する性質の考え方が徐々に明らかになっていくことになります。そこに登場するのが、コペルニクス(1473-1543)です。
著書『天体の回転について』の中で、彼が地動説を発表したのが1514年のことです。ところが、地球が動いていることをにわかに信じがたいとする批判にさらされます。
そしてガリレイ(1564-1642)は、慣性運動には外力が必要ないことを明らかにし、太陽を中心とする地球の円運動こそ外力を必要としない慣性運動と考えることで、コペルニクスの考え方の正しさを示そうとしました。
デカルト(1596-1650)は幾何学的考察から等速直線運動でなければ慣性運動にならないこと、そして円運動には外力が必要であることを明らかにしました。
デカルトとガリレイは落下運動の理論に慣性の考え方を適用し、落下距離、落下速度と落下時間の関係を考察しました。
二人とも落下運動の原因は引力、すなわち地球が物体を常に引きつけていることにあると考え、ガリレイは実験によって落下距離が落下時間の2乗に比例することを見つけ、デカルトは幾何学的考察から落下速度は落下時間に比例することを証明しました。
universo é scritto in lingua matematica(宇宙は数学の言葉によって書かれている)
(ガリレイ)

ケプラーの大発見
かくして運動の議論は惑星運動に集約されていき、コペルニクスから約100年後の1619年、膨大かつ精確な天体観測データが法則へと結実しました。
ケプラー(1571-1630)による惑星の運動法則の発見です。
- 第1法則:楕円軌道の法則
- 第2法則:面積速度一定の法則
- 第3法則:惑星の公転周期の2乗は、楕円軌道の長半径の3乗に比例する
まさにガリレイの言葉どおり、惑星の運動は数学の言葉で記述されるに至りました。
これによって地動説の優位が決定的なものなると同時に、コペルニクス、ガリレイらによる惑星の円運動の考えから脱却でき、はるかに正確に惑星の運動を記述できるようになりました。
ケプラーの名前が冠された数式が「ケプラー方程式」です。ケプラーは惑星の位置観測から軌道を推算しようと努力した末に3つの法則を得ました。しかし、ケプラー自身その目標を達成することはできませんでした。
それは、「太陽の周りを回る惑星の位置を時間の関数で表せるか」という問題です。
この難問を見事に解いてみせたのが、19世紀の天文学者であり数学者のベッセル(1748-1846)です。17世紀のケプラーから19世紀のベッセルまで一気に飛んでいってしまいました。
ベッセルがケプラー方程式を解くために必要だったのが18世紀のニュートンの運動理論です。
ニュートンの運動方程式
24歳のニュートン(1643-1727)が著書”Philosophiae Naturalis Principia Mathematica”(『自然哲学の数学的諸原理(プリンキピア)』)の中で運動についての画期的な理論を発表したのが1687年のことです。
ケプラーの法則が発見された1619年の68年後のことです。
ニュートンは新しい数学──微分積分学とともに星の運動についての新しい理論を建設しました。
万有引力の法則、木から落ちるリンゴとともに有名になったアイディアの核心は「運動」についての革新でした。
![]()
ニュートンの運動方程式
アポロのロケットが月に人類を運んだのも、大型タンカーが四海を安全に航行できるのも、F1のレーシングカーが極限の地上走行を実現したのも、あれもこれもこのニュートンの方程式のおかげです。
ここにmは物体の質量(kg)、Fは物体に働く力(N、ニュートン)、そしてaは物体の加速度(m/s2)を表します。
議論されてきた「運動論」は「力」の厳密な定義の完成により、「力学」と呼ばれるようになりました。
「ニュートン力学」の誕生により、アリストテレスの運動論は頂点に達することになりました。
20世紀にアインシュタインの相対性理論が生まれ、ニュートン力学が「古典力学」と呼ばれるようになった今日でも、わたしたちの身のまわりは「ニュートン力学」で十分に説明でき、大いに役立っていることに驚かされます。
これが「ケプラー方程式」の解法にとってキーとなる理論です。
微分とは勢いのこと
ニュートンは謎だった「力」を数学の言葉──微分で表すことに成功しました。
先に、微分とは刻々変化する運動の様子──瞬間(微かな時間)を定量化する技といいましたが、もう少し詳しく説明してみましょう。
私は小学生のときに“微分”に出会っていました。
ラジコンカーのディファレンシャル・ギア(differential gear)です。大型トラックを後ろから見ると後輪タイヤのシャフトの真ん中に大きな丸い形をしたものです。
差動装置と訳されるように、differentialは差という意味です。車は曲がる際に内輪と外輪に回転差が生じます。
左右両輪を同じ回転数で回転させてしまうとスムーズに曲がれません。そこでギアを組み合わせることで回転差をつけるのがディファレンシャル・ギアです。
数学の微分もおなじディファレンシャル(differential)なのです。微分方程式はdifferential equationです。
なぜ、微分が差と同じ言葉で表されるのか数式を使わないでざっくり説明してみます。
微分とは勢いのことです。
人であればやる気と言い換えることができます。車の微分が大きいとは、すなわち勢いが大きいことです。車の勢い──微分とはスピードです。
勢いをいかに計るのかが問題です。それには、現在を基準に少しだけ過去か、少しだけ未来と現在とある量を比べればいいのです。
そもそも車のスピードとは、瞬間のスピードです。スピード(速さ)とは移動距離÷かかった時間のことですから、瞬間のスピードとは瞬間の移動距離÷瞬間のことを表します。
移動距離が位置(座標)の差に他なりません。瞬間の位置(座標)の差(differential)が車の瞬間のスピードを表すことになります。
これが微分がdifferentialと訳される理由です。微分記号d/dtのdはdifferentialのことです。
微分記号d/dtを用いて、瞬間のスピードvは次のように表されます。
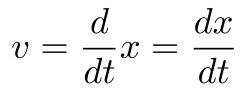
dtが瞬間(“微”かな時間)、dxは瞬間に移動した距離、それらの比(“分”数)であることから微分という日本語が理解できます。
加速度は速度の微分
すると加速度aの理解はあっという間です。車に乗っている時に体に力を受けるときを思い出してみましょう。
アクセルを踏んで発進する場合とブレーキを踏んで止まる場合がわかりやすいです。
体に力を受けるので体が後ろにふんぞり返るか前のめりになります。アクセルを踏んでいるときは、スピードがどんどん大きくなっているときです。
この瞬間のスピードの差をスピードの微分が加速度です。アクセルを踏むとき加速度は正で、ブレーキを踏むとき加速度は負になります。
この車の中の状況──力と加速度──を表したのがニュートンの運動方程式です。
速度が変化すると、加速度aが発生し、体(質量m)が受ける力Fは加速度と質量のどちらにも比例します。
急にアクセルを踏んだり、ブレーキを踏めば加速度は大きくなり体に受ける力Fも大きくなります。また体重が重ければ受ける力Fも大きくなります。
高速自動車道でスピード100km/hという大きな速度一定で走行していても体には力を受けません。速度の変化(差)が0つまり加速度が0なので力F=ma=m×0=0ということです。
再びガリレイ(1564-1642)の言葉を思い出してみます。
universo é scritto in lingua matematica(宇宙は数学の言葉によって書かれている)
(ガリレイ)
ガリレイは数学が進化していく言葉であることを理解していたことでしょう。
手が届かず見ることさえ容易でない天上界の星を捉えるために、私たちは数学という言葉を見つけてきました。
重力とはニュートンの万有引力のことです。ニュートンは月とリンゴに働く力に本質的な違いはないことを見抜き、天上界と地上界の統一を数理的に成し遂げた天才だったのです。
ニュートンは天体の軌道が楕円、双曲線、放物線に分類されることも発見しました。ニュートンは光学にも多くの業績を残しています。
光のスペクトル分析、ニュートン式反射望遠鏡の製作、光の粒子説、白色光がプリズム混合色であるとして色とスペクトルの関係についてなど。虹の色数を7色だとしたのもニュートンです。
「星と人とともにある数学」を実践した天才ニュートンが作り出した微分方程式という世界はさらに「運動」を解明していくことになります。

