オイラーゼータ関数 誕生物語

バーゼル問題

次に紹介するのは、今から300年前に大問題になった分数のたし算です。

分子が1で分母が自然数のべき乗の形をした分数を無限に足し合わせる「無限級数」の和を求める問題です。

I₁が調和級数、I₂がバーゼル問題と名前が付くほど、それぞれ歴史的に由緒ある問題です。

微積分学を作り出したドイツの数学者ゴットフリート・ライプニッツがこの世を去ったのが1716年。その後継者がスイスのベルヌーイ兄弟です。

兄ヤコブ・ベルヌーイ（1654-1705）の無限級数に関する論文の中で弟ヨハン・ ベルヌーイ（1667-1748）が、調和級数I₁が発散つまり答えが無限大になることの証明に成功しました。

そしてクローズアップされたのが無限級数I₂です。ライプニッツでも解けなかったその問題は、ヤコブに敗北宣言をさせるほど難問でした。

ヤコブがスイスのバーゼルの町で書き上げた『無限級数の扱い』には次のように書かれています。

もし、誰かが私たちの努力から逃れていた発見をして報告してくれたなら、私たちはその人に大いに感謝します。

『無限級数の扱い』（ヤコブ）より

ヤコブですら、I₂が2よりも小さい数値に収束することを突き止めるのがやっとでした。結局、ベルヌーイ兄弟はその真なる値にたどり着くことはできませんでした。

いったい誰が、無限級数I₂の中にsin、log、e、微分積分が隠れていることを想像したでしょうか。

いつしか無限級数I₂は「バーゼル問題」といわれるようになりました。

しかし、結果的にヨハンのおかげで「バーゼル問題」は解決することになります。解決した人物の師がヨハンだったからです。

オイラー登場

牧師になろうとしていた少年はヨハンと出会い数学の道を歩み始めました。その少年こそ18世紀最大の数学者レオンハルト・オイラー（1707-1783）です。

14歳になったオイラーはヨハンがいるバーゼル大学に入学しました。両親とも聖職者であったオイラーは牧師になることを運命づけられていました。

たぐいまれなる言語能力、暗記力、そして計算力を備えたオイラーは、バーゼル大学で神学とヘブライ語を学んでいました。

そんな中、オイラーはヨハンと運命の出会いをします。数学者ヨハンの後ろ姿は、オイラーの心を数学へ傾注させるに十分な魅力を持っていました。

天才だけが知り得る天才。天才ヨハンは神童オイラーの数学の素質を見抜き、熱心に指導しました。かくして数学者へと成長したオイラーの手によって「バーゼル問題」は解かれました。

時に1735年。

28歳のオイラーの手計算の風景に、sin、log、e、微分積分がどのように流れていくのか、そしてその終着駅で遭遇する驚異の景色をぜひ見届けていただきたいと思います。

収束が遅いバーゼル問題

そもそも、バーゼル問題は分数のたし算です。

次の計算を見てください。

ここから見えてくることは、単純なたし算すら困難であることです。そして、もし分数のたし算をある程度の項まで計算できたとしても、さらなる困難にぶつかります。

電子計算機に計算を肩代わりしてもらうと、初めから50項までの分数の和が1.62513、100項までの和が1.63498、そして和が1.64を超えるのに203項のたし算が必要なことがわかります。

無限級数I₂の項は正の数ですから、たし算する項を増やせば和も大きくなります。ところが、項を増やしていっても和は少しずつしか大きくなりません。

このような状況を収束の速さが遅いといいます。

いったいどこまで足せば収束値が見えてくるのか、このままの計算を続けていては（そもそも手計算で行うこと自体困難）希望の光をつかむことは絶望的なのです。

収束値を突き止めろ

オイラーは収束が遅い無限級数I₂を、収束が速い式に変形するアプローチをとりました。

そこでオイラーが用いた数学が、ネイピア数eを底とする自然対数logexと微分積分です。

はたして、収束が遅い無限級数I₂を“高速化”した無限級数の式にチューンアップすることに成功し、収束値を得ました。

ここからの計算の詳細は込み入ったものになります。テンポよくポイントの式だけを追っていきましょう。

オイラーが目を付けたのが、自然対数のマクローリン展開した数式です。

この式を素材として調理することで、無限級数I₂を作り出すことができます。

次がそのレシピです。

こうして調理されたオリジナルとは異なる姿に変身した無限級数I₂は“高速版”I₂と呼ぶにふさわしい式です。

無限級数I₂のオリジナル版は第200項まで足しても1.64になりません。それが“高速版”を用いれば、たった第4項までの計算でそれを越えてしまいます。

驚くべきことに、第15項までの計算（手計算可能）で収束値が小数第5位まで捉えることができる高速ぶりです。ついに、バーゼル問題が収束する風景が現れてきました。

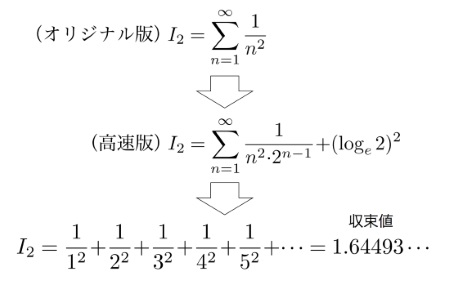
オイラーは獲物～収束値～の正体を捉えることに成功しました。無限級数I₂の収束値は1.64493…！

ここまでだけでも前人未踏の計算と言えますが、真に驚くべきオイラーの計算はこれから始まります。

1.64493に見覚えがある！？

オイラーは、眼前に現れた1.64493という数値を眺めながらつぶやきます。

「1.64493は円周率πの2乗を6で割った数値に違いない！」（予想）

いったい誰が1.64493を眺めて、それはπの2乗を6で割った数であるなどと見抜けるというのでしょうか。

ついにたどり着くバーゼル問題の原風景

オイラーが実際に計算した収束値は1.644934066847494です。π²/6＝1.644934066848226…と小数点以下11桁まで一致しています。

この驚くべき一致にオイラーは、バーゼル問題の収束値はπ²/6に違いないと確信しました。

オイラーはバーゼル問題の最後のチャレンジ～（予想）の証明～に挑みます。

なぜ、バーゼル問題の原風景にπがあるのか？

ここでオイラーが選んだ最初の式は、三角関数sin xのマクローリン展開です。無限級数I₂の“高速版”にチューンアップする際にとった方法が定積分Iを「2通りに表す」ことでした。

オイラーはここでも「2通りに表す」戦術をとります。三角関数sin xをマクローリン展開した式は「たし算」の形をしています。オイラーは三角関数sin xを「かけ算」の形に変形できないかと考えます。

sin x=0となるx（これを零点という）を利用すれば、それが可能になります。

こうしてすべての準備が整いました。2通りに表したsin x/xをイコールで結び、両辺のx²の項の係数を比較することで、終着駅～（予想）～が現れてきます。

かくして、オイラーは自らの予想を証明しバーゼル問題に終止符を打ちました。

しかしながら、いますべての期待に反して、私はバーゼル問題の値についてエレガントな表示を求めることができた。それは円周に依存している・・・私は、この級数の和を6倍したものが直径1の円の円周の平方に等しいことを発見した

以上の詳細な証明は拙書『感動する！微分・積分』（朝日新聞出版）で読むことができます。

ウルトラたし算　ゼータ関数の誕生

バーゼル問題は、分子が1で分母が自然数の2乗の分数を無限にたし合わせる問題です。

オイラーは分母が4乗，6乗，8乗と偶数乗の問題もバーゼル問題と同じように収束値を求めました。

すると、おもしろい法則が浮かび上がってきました。収束値のπも4乗，6乗，8乗になるのです。

オイラーは手計算の喜びを思い存分味わいながら計算の旅を続けました。分母が26乗までの計算を続けています。

オイラーによるバーゼル問題の劇的な解決をみることなく、兄ヤコブ・ベルヌーイはこの世を去ってしまいました。

弟ヨハンの言葉です。

「Utinam Frater superstes effet !　もし私の兄が生きていたなら！」

バーゼル問題の解決のために、青年オイラーはその時、持てるだけのものを全投入しました。sin、log、ネイピア数e、微分法、積分法、そして数学への情熱を。

数の世界の大冒険のエピローグに待ち構えていたのが、円周率πという驚きの風景でした。

オイラーはバーゼル問題を掘り下げていくことで、偉大なる数学にたどり着きました。オイラーのゼータ関数（オイラーゼータ）です。

積分法が無限に分割したものを無限にたし算する“スーパーたし算”ならば、ゼータ関数は“ウルトラたし算”と呼べるでしょう。

数学史上最大の難問「リーマン予想」は、オイラーゼータが導いた問題です。

連載は、ウルトラ計算～ゼータ～が見せてくれる驚異のたし算の風景を辿っていきます。

1614年　ネイピアの対数Logarithms誕生

【121年後】
1735年　バーゼル問題解決　オイラーゼータ誕生

【124年後】
1859年　リーマンゼータ誕生　リーマン予想

【157年後】
2016年　リーマン予想未解決