マクローリン展開｜三角関数のマクローリン展開の計算

sin31°の算出方法がわかった！？

高校2年生のとき、ある数学の問題の解法を探していることがきっかけで「マクローリン展開」に出会うことになりました。

この数式との出会いは衝撃的かつ大きな影響を与えるものでした。

まずは結論を急ぎましょう。この数式を用いることで懸案であったsin31°の数値を計算してみます。

マクローリン展開の式の特徴は多項式であることです。つまり、マクローリン展開を使うと、一般の関数を多項式で近似することができます。

xのべき乗を階乗（！）で割った値を数項たし算（ひき算）すればいいので、すべての計算は四則で可能です。

はたして、マクローリン展開はsin31°を0.515039とはじきだします。電卓の表示「0.515038074」と小数点以下5桁が合っているではありませんか。

この結果により、私は「電卓の中にプログラミングされているのはマクローリン展開ではないか」と考えました。

弧度法

三角関数のマクローリン展開の数式を用いる際には準備が必要です。

角度を「°」から「rad（ラジアン）」に変換する計算 ── 弧度法です。xに31°を代入することはできないのです。

なぜわざわざ角の開き具合である角度を「°」ではなく「rad」とする必要があるのでしょうか？

1°は1周を360分割した量、すなわち360°が1回転を表すように定義された量です。360という数値の起源は、1年＝365日、すなわち地球の太陽の周りを回転する公転周期です。

1次関数y=xや2次関数y=x²のxとはどのような量なのかを考えることから始めてみます。

明らかにx軸上原点からの「長さ」「距離」を表しています。角度という量もこのx²のxと同じように長さで表すことを考えるのです。

グラフで考えてみるならば、1次関数y=xや2次関数y=x²が描かれたところに、xを「°」にしたままで三角関数y=sin xのグラフを描くことができません。

xが「長さ」「距離」を表していないからです。三角関数y=sin xのxを「長さ」「距離」として扱えるようにします。角の大きさの測り方を分度器から定規にすればいいのです。

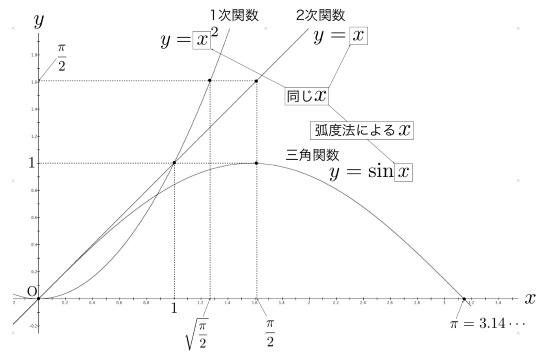
いま、わかりやすく半径を1[m]と長さの単位をつけて表しておきます。1周の長さは直径×円周率＝2π[m]なので、次の関係がわかります。

1周：360° ↔ 2π[m]

同様にして次のような計算もできます。

半周：180° ↔ π[m]
4分の1周：90° ↔ π/2 [m]

これから、360°の代わりに2π、180°の代わりにπ、90°の代わりにπ/2を用いることできます。

このような、角の大きさを単位円（半径1の円）の弧の長さに置き換えるという考え方を「弧度法」、角の単位を[rad]と呼びます。

したがって次のような関係になります。

360° ↔ 2π[rad]
180° ↔ π[rad]
90° ↔ π/2 [rad]

三角比が三角関数へ変身

この弧度法のおかげで、三角比は晴れて三角関数へと変身します。その最大の恩恵こそ微分法が適応されることです。

マクローリン展開は与えられた関数を微分することで得られます。

31°をradに変換してみましょう。

2π[rad]=360°の関係から、1[rad]=(360/2π)°=約57.3° または、1°=(2π/360)[rad]= 0.01745328…[rad]とわかります。

したがって、次のように計算されます。

31°=0.01745328…× 31[rad]≒0.541052[rad]

この値をマクローリン展開の式のxに代入して、sin31°が計算できます。