目次
音楽とフーリエ級数
フーリエ級数。
私がその言葉に出会ったのは中学生の時。シンセサイザー奏者・作曲家である冨田勲（1932-2016）のアルバム『宇宙幻想』のライナーノーツの中での出会いでした。
突如現れた数式とフーリエ級数という言葉に感激したことを鮮烈に記憶しています。
ストラディヴァリウスのヴァイオリンと、近代の工場で作られる楽器のどこがちがうのか。この秘密を解き明かす数学物理的道具は1つしかない。
フーリエの級数理論といわれているこの式である（数学アレルギーのある方は、詩の一節だと思って眺めていてください）。
f(x)＝…でなく、f(x)⇆…と書いてあるところがミソである。f(x)→ の方はf(x)が、ストラディヴァリウスならば、その音の秘密を「分析、解析」した結果が、右辺の各項である。
【出典】『宇宙幻想』（冨田勲）ライナーノーツ
音楽の主人公は音という波。そして、星の探究から生まれた三角関数（sin・cos）。音楽レコードと数学はそれほどかけ離れた関係ではありません。
今回はその「フーリエ級数」に迫っていきます。
フーリエ、1807年の主張
フーリエの主張は次の通りです。
任意の関数は、三角関数の無限級数で表すことができる。
この「三角関数の無限級数」が「フーリエ級数」に他なりません。
数式で表現すると次のようになります。
フーリエ級数
この右辺がフーリエ級数です。
ちなみに、上記ライナーノーツの数式右辺第1項の分数の分母「z」は誤りで、正しくは2です。
フーリエの主張は次のように言い換えることもできます。
任意の曲線は、正弦波と余弦波の合成で表すことができる。
百聞は一見に如かず。さっそく結論を見てみましょう。
1次関数f(x)=x（グラフは直線）をフーリエ級数で表した場合の様子が次のグラフです。
上のグラフは三角関数10項の和です。グラフが波打っている様子が分かります。
これに対して下のグラフは三角関数100項の和です。グラフは両端付近以外では直線になっていることが分かります。
項数を大きくしていくと直線に近づいていきます。このことが、1次関数（直線）が三角関数の無限項の和（これをフーリエ級数という）で表されるという意味です。
複雑な関数は単純な波動、すなわちsinとcosの和として表現されるというのがフーリエ級数の理論です。
フーリエはフーリエ級数の研究から「フーリエ変換」というさらに画期的な成果を得ます。
sinとcosのおかげで、フーリエ級数に現れるそれぞれの波の量を積分によって復元できることをフーリエは発見しました。
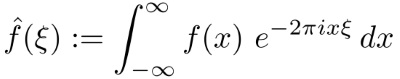フーリエ変換
この数式で重要なのは、連載でも紹介した「オイラーの公式」です。
オイラーの公式
このsinとcosを合わせ技にしたネイピア数eを用いることで、フーリエ級数をうまく記述できます。
フーリエ変換の数式において変数xは時間を表し、変数ξは周波数を表します。フーリエ変換とは「波を周波数ごとに分解する」演算と解釈できます。
特定の周波数のレベルを棒グラフで表すスペクトラムアナライザーは、フーリエ変換の応用です。
ジャン・バティスト・ジョゼフ・フーリエ
1768年、フーリエはフランスのオセールで仕立屋の息子として生まれました。8歳の時に孤児になり、地元の司教のもとに預けられました。
士官学校に入学したフーリエは数学に興味を持ち始め、勉学の励むようになりました。貧乏な身分のため軍人の道を閉ざされたフーリエは、修道院に入れられました。
しかし、1789年のフランス革命により自由の身となったフーリエはパリへ向かい、数値方程式の近似解を計算する方法を論じた論文をパリ科学アカデミーに提出します。
数学教師になったフーリエは革命委員会のメンバーとなり、委員長も務めることになりました。
この時期はいわゆる恐怖政治です。要注意人物としてマークされ、政治的弾圧を受けながらもフーリエはなんとか生き延びました。
1794年にフーリエはパリのエコール・ノルマル・ジュペリュール（高等師範学校）入学。そこで数学者ラグランジュやモンジュといった大数学者に認められ、エコール・ポリテクニークに就職しました。
1798年にナポレオンのエジプト遠征に文化関係の仕事の一員に選ばれ、モンジュらとともに従軍しました。
有名な『エジプト誌』の監修を行ったのがフーリエで、あのロゼッタ・ストーンをエジプトから持ち帰ったのもフーリエでした。
帰国後、フーリエはナポレオンに行政手腕を認められ、イゼール県の知事に任命されました。新しい道路を作り、学校教育の改革などを行い行政的手腕をふるいました。
この時、フーリエは12歳のシャンポリオンにロゼッタ・ストーンを見せています。のちに彼が20年をかけて解読することになりました。
フーリエが生涯で最も精力的な研究活動を行ったのがこの時期でした。最高傑作である論文『熱の解析的理論』を完成させ、この中でフーリエ級数が登場します。
世界は波でできている
最も原始的な存在が波です。人類は波を巧みに生活に取り入れて活用することで文明を発展させてきました。
音楽という芸術もすべては波に始まり波に終わる世界です。楽器の振動は空気の振動──音波となり、空気の振動は聴覚器官である耳でキャッチされ、その信号は電気信号に変換され神経組織を伝わり脳に送られて、高度な意味認識処理がなされます。
音波は鼓膜を通って中耳、内耳へと伝わり、蝸牛（かぎゅう）という螺旋状の構造をした部分に到達します。この螺旋は先端に向かって次第に細くなる構造をしています。
蝸牛にある有毛細胞はその位置する場所によって、分析する音の周波数が違います。蝸牛の入り口付近では20000Hz位の高い周波数の音が分析され、奥に向かうにつれて低い周波数の音の分析がなされます。
音波はそれぞれの場所にあるリンパ液を振動させ、その振動を有毛細胞という細胞がキャッチして脳に信号を送ります。
この蝸牛の役割こそがまさに「波を周波数ごとに分解する」という働きで、音の信号は脳に送られる前に「フーリエ変換」処理が行われていることになります。
こうした聴覚を持った私たち人間が楽器を作り、音楽という芸術を作り上げることができました。
シンセサイズとは合成するという意味です。合成装置を意味するシンセサイザーとは、電気的に作り出された音波に対してさまざまな処理を行うことで、新しい音を合成する楽器です。
シンセサイザーの世界では、信号処理がアナログ（アナログ・シンセサイザー）からデジタル（デジタル・シンセサイザー）に進化して、日進月歩の様相を呈しています。
日本の楽器メーカーはとりわけ独創的なシンセサイザーを世界に提供しています。
PCM（パルス符号変調）やDSP（デジタルシグナルプロセッサ）といったデジタル信号処理技術が、アナログとデジタルを結び付けることを実現しています。
さらにインターネットの発達は高度な圧縮技術に支えられています。
波の情報──映像は光という波、音楽は音──はすべてデジタルに変換され、JPEGやMPEGといった圧縮方式によって適度な大きさの情報量に圧縮されるおかげで、インターネットの伝送が可能になります。
こうした技術の積み重ねで、誰もが映像音響作品を自由に制作し堪能できる時代になりました。これらすべての過程（耳、シンセサイザー、信号処理、圧縮技術）に三角関数が深く関わっています。
世界は波でできている。
物質世界の根源を探る理論「量子力学」は、存在の根源を「粒」と「波」で説明します。ここでもフーリエの理論が重要な役割を果たしています。
ナポレオンとともに激動のフランスを生き抜いたフーリエ。その革命戦士は数学という最強の武器をもって社会のために闘い抜いたのです。
現在、CD・DVD・インターネットを通して映像音楽作品に接する時、五感で感じる波動の中に音にならない通奏低音を感じることができます。
三角関数という目に見えない数学と数学者フーリエの心の波動です。
数学は、われわれの感覚の不完全さをおぎなうため、またわれわれの生命の短さをおぎなうために呼び起こされた、人間精神の力であるように思われる
（フーリエ）
ジャン・バティスト・ジョゼフ・フーリエ男爵（1768-1830）
アルバム「宇宙幻想」のライナーノーツを書いた人物
随想と題して、冨田勲のアルバムに寄せた文章を書いた人物こそ、日本の宇宙開発・ロケット開発の父・糸川英夫（1912-1999）です。
糸川はロケットの研究だけでなく、バレイ・チェロ・ヴァイオリンにも興味を持っていました。
驚くべきことに、ストラディヴァリウスの音の合成を研究していたほどの熱の入れようでした。つまり、シンセサイザーの製作にチャレンジしていたのです。
ライナーノーツの中で「トランジスターの進歩による驚異的な電子音響技術をフルに駆使して、私の夢を現実した人がいる。冨田勲氏である。」と綴っています。
そして、以下の文章で結んでいます。
トミタ・シンセサイザー・ミュージックの、数学的、技術的根拠をつくったフーリエという数学者は1768年、フランスで生まれ1830年に死亡し、一生の間ナポレオンと運命を共にした。
（中略）
フーリエは、バッハの死の直後に生まれ、ワーグナーの生まれる頃に死亡した。
人類の文化の歴史の興味深い綾の1つのように思えるのではないだろうか。
【出典】『宇宙幻想』（冨田勲）ライナーノーツ
