前回のシルエットパズルの解答は以下になりますが、この記事を初めてご覧になった方は、まず「清少納言知恵の板」に挑戦してみてください。


「清少納言知恵の板」は正方形を分割した7つのパーツを用いてさまざまな形をつくるシルエットパズルでした。
今回はその逆で、正方形をつくる江戸のパズル「裁ち合わせ」を紹介します。
目次
『勘者御伽双紙』寛保3年(1743)の裁ち合わせ

「裁つ」とは、衣服に仕立てるために型に合わせて布地を切ることを意味します。裁ち合わせは長方形の紙を切って、正方形をはじめ様々な形をつくる問題です。
さっそく『勘者御伽双紙(かんじゃおとぎそうし)』の問題にチャレンジしてみましょう。
横縦の長さの比が1:2の長方形を裁ち正方形にせよ、とあります。

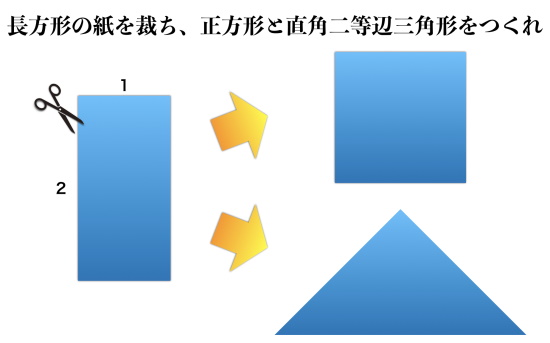
『勘者御伽双紙』(上巻)にある裁ち合わせ問題
次のような解答が紹介されています。

『勘者御伽双紙』(上巻)裁ち合わせ問題の解答
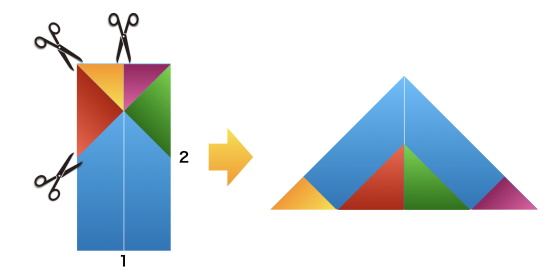
『勘者御伽双紙』(上巻)裁ち合わせ問題の解答
『勘者御伽双紙』では、裁ち合わせの問題が14ページにわたり載っています。






数学者 中根彦循
著者である中根彦循(なかね げんじゅん、1701-1761)の父は数学者中根元圭(なかね げんけい、1662-1733)。
父・元圭は数学者建部賢弘(1664-1739)に師事。建部賢弘が将軍吉宗の学問顧問であったことから、吉宗の命で「暦書全書」(梅文鼎(ばいぶんてい)著)の翻訳を完成し、伊豆下田で太陽・月の観測を行い貞享暦の正確度を調べています。
息子の彦循は京都の数学者で、父と同じく建部賢弘に師事し、後に京都で数学を教えました。著書『勘者御伽双紙』は古くから伝わる数学遊戯や中国数学、和算の面白い問題を集めたものです。
現在でも知られる小町算は、元々田中由真著の『雑集求笑算法』に通小町九十九夜として最初の紹介がありました。これを彦循が『勘者御伽双紙』の上巻の冒頭で小町算として引用し今日に至っています。
高次方程式の近似解法を研究していた彦循は、この本にもそのことを盛り込んでいます。
『勘者御伽双紙』中巻、三十三 女子(めのこ)平方の事には、まず25の平方根が5であることが説明され、次に11の平方根が3.316であることが解説されています。
3.316×3.316=10.995856
であることから近似値としては正しい。
この平方根算出アルゴリズムはたし算を用いています。そのため、20世紀になって発明された初期の計算機(タイガー計算機やカシオのリレー式計算機)が平方根を求めるアルゴリズムとして使われています。


『勘者御伽双紙』中巻 三十三 女子平方の事
『改算記』万治2年(1659)の裁ち合わせ
1627年吉田光由によって生みだされた数学書『塵劫記』は江戸時代の最大のベストセラー書籍となりました。
1659年、山田正重(生没年不明)は『塵劫記』をはじめ『参両録(さんりょうろく)』(1653)、『因帰算歌(いんきさんか)』(1640)などの数学書の誤りを正した『改算記』を著しました。

山田正重著『改算記』(1659)
この本にある裁ち合わせ問題にチャレンジしてみましょう。

『改算記』横三尺二寸縦五尺の紙を裁って正方形にせよ

『改算記』横32cm縦50cmの紙を裁って正方形にせよ
ヒントは面積。32×50=1600。これを正方形にした場合、1辺40の正方形となります。
つまり、
32×50 → 40×40
これらをじっくり眺めていると答えが見えてきます。
8×10の小さい長方形を考えることで次のような裁ち方が考えられます。
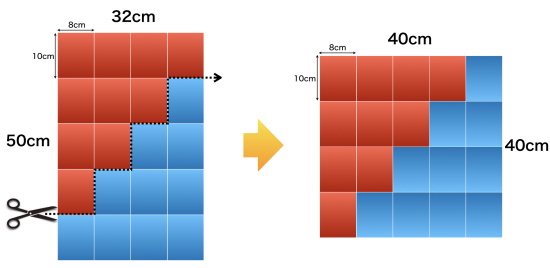
『改算記』裁ち合わせ問題の解答
では次の問題にチャレンジしてみてください。解答は次回紹介します。

