
目次
驚異のたし算
「オイラーゼータ関数誕生物語」では、長年懸案であった無限級数──無限の項のたし算──「バーゼルの問題」が28歳のオイラーによって解決される様子を描きました。
結果にπが描き出される風景とその華麗なる証明は世界に激震を与えました。
オイラーは、バーゼルの問題の背後にある原風景──ゼータ関数(オイラーゼータ)に到達し、その風景を次々に描き出していきました。
中でも次の絵は衝撃的です。

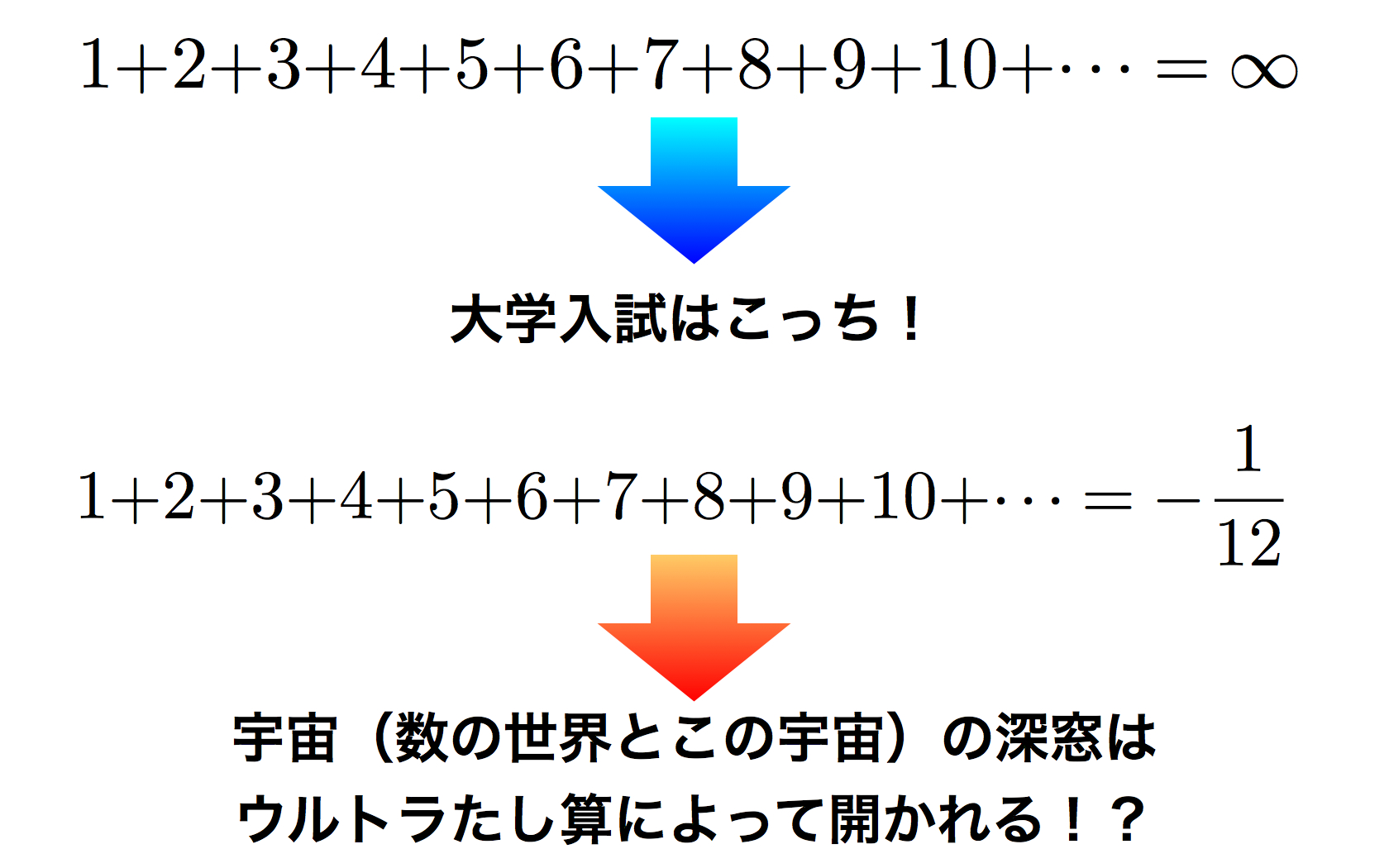
無限項の自然数の和がマイナスになるという信じられないたし算です。
私がゼータ関数を“ウルトラたし算(UT:Ultra Tashizan)”と呼ぶ理由です。このたし算を「UT1」と名付けることにします。
UT1と宇宙の関係
私は大学2年生の時、数学のUT1が物理学に関係していることを知りました。時空の根源を構成する物質と力のすべてを素粒子に還元して説明するのが素粒子理論です。
そこでは4つの力(重力、電磁気力、弱い力、強い力)を最終的に一つの力に統一することが大きな目標とされます。
超弦理論はその万物の理論(TOE:Theory of Everything)の最有力候補です。最小構成要素を点の代わりに弦にする理論は、驚くべき進展を見せました。
超弦理論の大きな特徴の一つが時空の次元が10であることです。
10次元時空=1次元時間+9次元空間
1984年、グリーンとシュワルツが発表した論文に衝撃の計算を見ることができます。
超弦の生息できる世界がなぜ10次元なのか?
それを導いたのがUT1です。

物理学を目指していた私に、数学こそ強力な武器であることを強烈に印象づけました。
UT1については、拙書『数学で宇宙制覇』(海竜社)や『リーマン予想がわかる』(日本評論社/黒川信重編著)でも紹介しています。
ウルトラたし算の衝撃
UT1以外のゼータ関数が描き出す驚異の風景を見ておきましょう。

UT0、UT1、UT2、UT3が一同に揃った異様な光景を見て、私はよく「ぷっつん数式」と言っていました。(1986年の流行語部門・大衆賞に選ばれた「ぷっつん」にちなんだものです。)
オイラーが18世紀にこれらを計算してみせたことを、物理学者たちはずっと「それは数学世界の物語」と片付けていたふしがありました。ところが突然ゼータが物理学に出現する事態になりました。
1984年に始まる超弦理論(UT1)そして、1997年にカシミール効果(2枚の金属版に働くゼロ点エネルギー)の理論値の計算に登場したUT3が実験で確認される“事件”が起きました。
超弦理論やカシミール効果といった物理学に突如姿を見せたゼータに、もはや数学は別世界だとそっぽを向いていられなくなったのです。
ウルトラたし算UT1の3つの証明
ここでUT1の証明を3つ紹介しておきます。

証明その1は、ゼータと関・ベルヌーイ数Bnの関係式を用いたものです。関とは我らが算聖・関孝和(1640頃-1708)です。

証明その2とその3は、ゼータの関数等式と呼ばれる関係式を用いたものです。
その2には、ガンマ関数、π、cosが、その3ではπとiが登場しています。どちらにも登場するのがバーゼルの問題ζ(2)=π2/6です。
61歳のオイラーは1768年の論文の中でUT1に迫る驚異の計算を行っています。バーゼルの問題を解決したのが28歳でしたから、30年にわたりゼータを計算し続けたことになります。

読者の皆さんは、同じたし算の2つの全く異なる結果をどう受け止めるでしょうか。
著者である私のもとには、年に数通、UT1についての質問が編集部経由で届きます。その反応は「受け入れがたい」という憤りを基本としたものです。
(数学の)問題には定義が含まれており、その定義に対して答えが定まるということです。
1+1=?という問題の答えは2、10、11、その他いくらでもあります。それは1という数と+とたし算の定義によるということです。自然数の1と+を通常のたし算とすれば、答えは2です。
2進数の1同士の和と+を通常のたし算とすれば、答えは2進数の10(10進数の2)です。1を文字列、+を文字列結合とすれば、答えは文字列11です。
1+2+3+…を自然数の通常のたし算とすれば、答えは∞(無限大)です。それに対して1+2+3+…をζ(-1)を経由すれば、答えは-1/12です。とはいえ釈然としない思いがあるかもしれません。
オイラーを受け継ぐ天才がその決定打を与えてくれるのです。リーマン(1826-1866)によって、UT1の証明を納得させる理論が打ち立てられます。それが、オイラーゼータを全複素数平面に解析接続したリーマンゼータです。
連載は「関・ベルヌーイ数 誕生物語」「リーマンゼータ 誕生物語」と続きます。
