東京タワーと東京スカイツリーが同じ高さに見える場所を空間情報で分析

東京タワーと東京スカイツリー。高さの違う2つの塔が同じ高さに並んで見える場所があります。

今回はその場所を空間情報分析の観点から考察してみたいと思います。

東京タワーと東京スカイツリーの高さ

かつて電波塔として日本一の高さを誇った東京タワー。

2012年5月22日の東京スカイツリー開業（竣工は2012年2月29日）によりその座を譲り渡しましたが、ふと、この2つのタワーが同じ高さに見える場所はどこだろうと考えました。

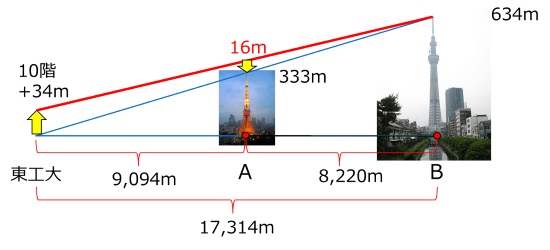
東京タワーは333メートル、東京スカイツリーは634メートル。両者は直線距離で8,220メートル離れています。

相似図形に着目

この問題は中学校の数学で習う「相似図形」に着目すると、簡単に解けます。

同じ高さに見えるということは、見上げる角度（仰角）が等しいということです（下図参照）。

ここで、地点P₁から東京タワーを見上げたときにできる三角形P₁ACと、東京スカイツリーを見上げたときにできる三角形P₁BDは相似であることに気づきます。

すなわち、各辺の長さの比にP₁A:P₁B=AC:BDという関係が成立しています。

同様に、仰角が等しい地点P₂からも同じ高さに見え、三角形P₂ACと三角形P₂BDは相似であることから、P₂A:P₂B=AC:BDという関係が成立しています。

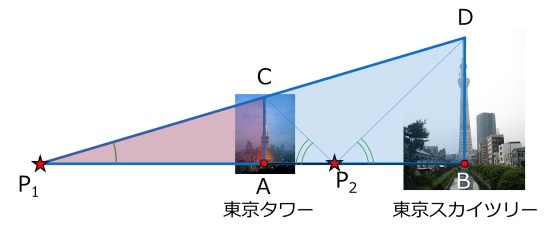
すなわち、PA:PB=AC:BDという関係が成立するような地点Pから見れば、2つのタワーは同じ高さに見えるはずです。

このような地点Pの集合は、P₁P₂を直径とする「アポロニウスの円」と呼ばれる円となります。

下図は、このアポロニウスの円を地図に落としたものです。

東京スカイツリーと東京タワーを通る半直線Lとアポロニウスの円が交わる地点に東京工業大学があります。

それでは実際に東京工業大学の西8号館に行って確かめてみましょう。

このとき注意したいのは、西8号館が半直線Lの南側にあることです。作図が正しければ、東京スカイツリーは東京タワーの右側に見えるはずです。

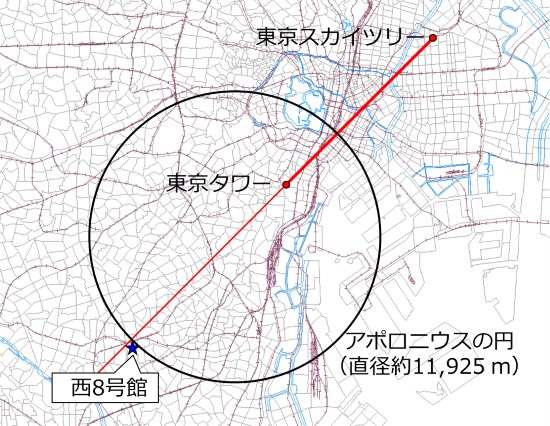
どうでしょう？

西8号館10階から見てみると、確かに同じ高さに見えますね！ しかも東京スカイツリーは右側に見えます。

今度は半直線Lよりも北側にある緑ヶ丘1号館から見てみましょう。東京スカイツリーは東京タワーの左側に見えるはずですよね？

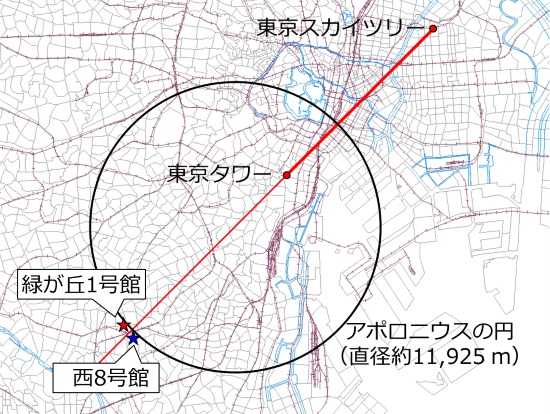
どうでしょう？

予想どおり東京スカイツリーは左側に見えます。

さらに、半直線Lへ接近して建っている緑が丘3号館から見てみましょう。

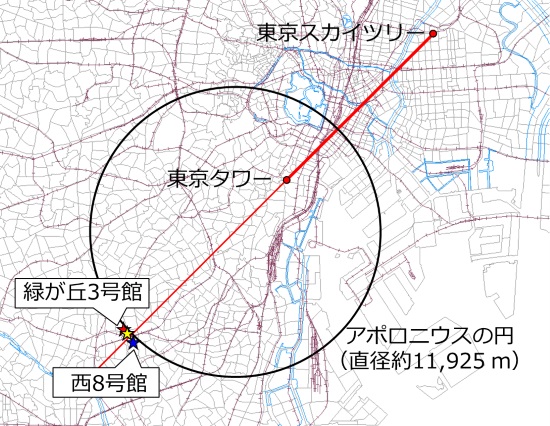
予想どおり2つのタワーは一段と近づきました。でも何か変です。

西8号館10階から見たときは同じ高さに見えましたが、緑が丘3号館4階からだと東京スカイツリーの方が低く見えます。

なぜでしょう？

視点の高さが影響するのか

どうやら見る位置（視点の高さ）が影響しているようです。10階と4階では、ずいぶん高さが違って見えるようですね。

しかしまたもや新しい疑問にぶつかります。

見る位置が高くなると、手前にある東京タワーが低く見えるはずです。

下図に示すように、ここでも相似の関係を利用すれば、東京タワーは約18m低く見えることになります。

ではなぜ西8号館10階から見たときは同じ高さに見えたのでしょうか？

地球は丸い！

「地球は丸い」ということを思い出せば理解できます。

これも中学校の数学で習う「ピタゴラスの定理（三平方の定理）」を使えば簡単に説明できます。

水平線の向こうから大きな帆船が近づいて来るのをイメージしてみましょう。船体は隠れたままで、マストの先端から見え始めます。

下図は、帆船までの距離をd、隠れている部分の高さをx、地球の半径をrで表したものです。

このときピタゴラスの定理（三平方の定理）を用いてxについて解くと、隠れて見えない部分の高さxは、地球の半径rと帆船までの距離dから簡単に求めることができます。

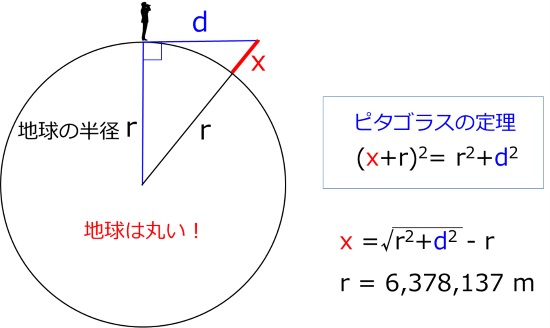
この式に地球の半径rと東京工業大学からタワーまでの距離dをそれぞれ代入してみると、東京タワーは約6m、東京スカイツリーは約23m、足元が隠れて実際より低く見えます。

西8号館10階から見ると、これに「視点の高さ」による影響（約16m）が加わり、東京タワーは約22m（＝6m＋16m）低く見えます。^（注）

すなわち、西8号館10階から2つのタワーが同じ高さに見えたのは、「視点の高さ」と「地球は丸い」ことの影響が上手くキャンセルされたためであることが分かります。

おわりに

普段わたしたちは地球が丸いことなど意識せずに生活しています。

しかし、広領域の空間情報を扱う際には決して無視できない重要な事実であることが分かります。

都市的なスケールで世の中を見渡してみると、いつもは見過ごしている興味深い事実に遭遇するかもしれません。

^（注）ここでは簡潔に説明するため、各地点の標高（西8号館：24m、東京タワー：8m、東京スカイツリー：1m）を無視して計算しています。

しかし標高差を考慮し、より厳密に計算しても、西8号館10階からの見かけ上の高さの差は同程度に小さな値となります。