
前編ではオイラーのゼータ関数のPythonコードmpmath.zeta()とオイラー積の簡単な説明を行いました。
後編ではオイラーの積計算用コード(5つ)とその計算結果を紹介します。
目次
コード1 「eulerpdoduct.ipynb」(Jupyter Notebook用)

まずはお手軽なコード1です。Jupyter Notebook用ですから気軽にオイラー積の計算を試してみることができます。
核になるコードはオイラー積の関数定義部分です。
>>> #【再帰的定義】ノーマル演算 任意精度演算 mp.mpf()なし
>>> def eulerproduct0(N):
>>> if N == 0:
>>> return 1
>>> else:
>>> product = 1/(1-1/(prime(N)**2))
>>> return eulerproduct(N-1)*product
>>>
>>> # 【再帰的定義】任意精度演算 mp.mpf()使用
>>> def eulerproduct(N):
>>> if N == 0:
>>> return 1
>>> else:
>>> product = 1/(1-mp.mpf('1')/(prime(N)**2))
>>> return eulerproduct(N-1)*product
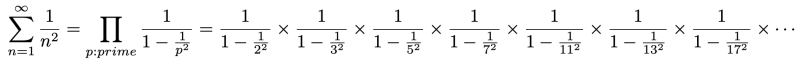
素数積product = 1/(1-1/(prime(N)**2)) の計算精度が心配なので、ノーマル演算のeulerproduct0(N)と任意精度演算mp.mpf()を使ったeulerproduct(N)の2つを定義しました。
前編でも説明したように、n番目の素数を与える関数sympy.prime(n)のおかげで面倒なコードが不要なのです。
コード1 実行結果
| ζ(2) = | 1.6449340668482264061(真値) |
| 10個の素数 mp.mpf()なし | 1.63307049049573921342651542005 |
| 10個の素数 mp.mpf()あり | 1.63307049049573922032524534874 |
| 100個の素数 mp.mpf()なし | 1.64451522172429361657641986079 |
| 100個の素数 mp.mpf()あり | 1.64451522172429375358545680644 |
| 1000個の素数 mp.mpf()なし | 1.64491317470634199212269796783 |
| 1000個の素数 mp.mpf()あり | 1.64491317470634198691867721661 |
| 2000個の素数 mp.mpf()なし | 1.64492523884727614514999850439 |
| 2000個の素数 mp.mpf()あり | 1.64492523884727613002462327701 |
素数の個数を10、100、1000と10倍に増やしていくと、ζ(2)の正しい値が1桁ないし2桁ずつ増えていくのがわかります。1000個の素数を使っても5桁を得るのがやっとであることがわかります。
それにしても、1000番目の素数prime(1000)=7919まで1000個の素数を使った積があっという間に計算できることに驚かされます。

コード2 「eulerproduct_zeta2_nolist.py」
コード2はコード1の通常Pythonコードです。
Jupyter Notebookでは2000個の素数の計算ができました。通常のPython(Python3.8とPython3.9で実行)で試してみると900個の素数までしか計算できませんでした。
皆さんのPythonでは何個の素数まで計算できるでしょうか。
>>> # eulerproduct_zeta2_nolist.py
>>> # ζ(2)=1.6449340668482264364724...のオイラー積による数値計算
>>> # 素数リストは使わず、sympy.prime(n)を使用
>>>
>>> from sympy import * # 数値計算 sympy.N()
>>>
>>> # 任意精度演算 桁数設定
>>> from mpmath import mp
>>> mp.dps = 100 # 小数点以下100桁
>>>
>>> # ゼータ関数ζ(x) = mpmath.zeta(x)
>>> from mpmath import zeta
>>>
>>> print('ζ(2)=1.6449340668482264364724...のオイラー積による数値計算 sympy.prime(n)利用')
>>>
>>> #【再帰的定義】ノーマル演算 任意精度演算 mp.mpf()なし
>>> def eulerproduct0(N):
>>> if N == 0:
>>> return 1
>>> else:
>>> product = 1/(1-1/(prime(N)**2))
>>> return eulerproduct0(N-1)*product
>>>
>>> print('\nノーマル演算 任意精度演算 mp.mpf()なし')
>>> print('ζ(2)=\t', N(zeta(2),30), '(真値)')
>>> print('10コ\t', N(eulerproduct0(10), 30))
>>> print('100コ\t', N(eulerproduct0(100), 30))
>>> print('900コ\t', N(eulerproduct0(900), 30))
>>> # print('1000コ\t', N(eulerproduct0(1000), 30)) # NG
>>>
>>>
>>>
>>> # 【再帰的定義】任意精度演算 mp.mpf()使用
>>> def eulerproduct(N):
>>> if N == 0:
>>> return 1
>>> else:
>>> product = 1/(1-mp.mpf('1')/(prime(N)**2)) # mpfはReal float用
>>> return eulerproduct(N-1)*product
>>>
>>> print('\n任意精度演算 mp.mpf()使用')
>>> print('ζ(2)=\t', N(zeta(2),30), '(真値)')
>>> print('10コ\t', N(eulerproduct(10), 30))
>>> print('100コ\t', N(eulerproduct(100), 30))
>>> print('900コ\t', N(eulerproduct(900), 30))
>>> # print('1000コ\t', N(eulerproduct(1000), 30)) # NG
コード3 「primelist_file_prime.py」
sympy.prime()を使ったコードでは2000個の素数が限界でした。そこで、別な作戦でオイラー積に挑んでみます。
素数リストをファイルに書き出して素数を使う方法です。これも実際にコードを実行してみるまではいくつ素数がつくれるかはわかりません。まずはsympy.prime()を使って素数リストのファイル作成をしてみます。
リストをファイルとして保存するために標準ライブラリpickleを使います。
primelist_file_prime.pyを実行すると、何個の素数をリスト化するのかきかれます。大きな数を入力できるようにするため、べき乗**が使えるようになっています。
nに対して、10**4を入力したとすると、10000個の素数リストがファイル名「primelist_10to_power4_ko.binaryfile」として保存されます。
これはバイナリーファイルです。テキストファイルのようにエディターで開いても、素数を確認することはできません。
素数2,3,5,…をそのままリスト化してファイル保存してしまうと、0番目の素数が2、1番目の素数が3となり使い勝手が良くありません。
そこで、素数リストの先頭(0番目)を1として、続けて2,3,5,…と素数を追加します。こうすることでファイルの1番目の素数が2となります。
>>> # primelist_file_prime.py
>>>
>>> from sympy import *
>>> import pickle
>>>
>>> a = input('sympy.prime()を使ってn個の素数リスト\nprimelist_n_ko.binaryfile を生成します。**使用可 n >> ') # a = 10**4
>>> n = eval(a) # n = 10000
>>>
>>> primelist = [1] # 素数のナンバリングを1スタートに合わせるため先頭0番目を1にしておく
>>> for i in range(1,n+1):
>>> primelist.append(prime(i))
>>>
>>> file = 'primelist_'+a+'_ko.binaryfile' # 生成するファイルのファイル名 primelist_10**4_ko.binaryfile
>>> file = file.replace('**', 'to_power') # ファイル名の**部分があればリネーム primelist_10to_power4_ko.binaryfile
>>> f = open(file,'wb') # リストをファイルに書き出し
>>> pickle.dump(primelist, f) # データ上書き
>>>
>>> # 生成されたファイルを読み込み
>>> f = open(file,'rb')
>>> primelist = pickle.load(f)
>>> # 内容チェック
>>> # print(primelist) # コメントアウト:nが大なら非表示、コメント解除:nが小ならリスト全出力
>>> print('\nデータ数',len(primelist),'個') # 全要素数出力
>>> print('0番目', primelist[0]) # 0番目のデータ出力
>>> print('1番目', primelist[1]) # 1番目のデータ出力
>>> print('最後', len(primelist)-1,'番目',primelist[len(primelist)-1]) # 最後のデータ出力
>>> print(file,'\nが生成されました。') # 生成されたファイル名出力
コード3 実行結果
私の環境では、10分ほどで10000個の素数リスト生成が限界でした。コード1の2000個よりも大きいので進歩しましたが、ちょっとがっかりです。
さらに多くの素数リスト生成をめざします。
コード4 「primelist_file_eratosthenes.py」
最後はsympy.prime()に頼らず、素数を一から生成します。
連載第7回でも紹介したエラトステネスの篩アルゴリズムによる素数生成です。単純にして意外に強力なアルゴリズムです。
>>> # primelist_file_eratosthenes.py
>>>
>>> from sympy import *
>>> import pickle
>>>
>>> a = input('エラトステネスの篩を使ってn個の素数リスト\nprimelist_n_ko.binaryfile を生成します。**使用可 n >> ') # a = 10**4
>>> b = int(eval(a))
>>> n = prime(b) # n番目の素数 sympy.prime(n)
>>> p = [i for i in range(n+1)]
>>>
>>> for i in p[3:]:
>>> if p[i] % 2 == 0:
>>> p[i] = 0
>>>
>>> # エラトステネスの篩アルゴリズムによる素数生成
>>> root_n = n**0.5
>>> for i in range(3, n):
>>> if i > root_n:
>>> break
>>> if p[i] != 0:
>>> for j in range(i, n + 1, 2):
>>> if i * j >= n + 1 :
>>> break
>>> p[i * j] = 0
>>>
>>> primelist = sorted(list(set(p)))[2:]
>>>
>>> # 素数のナンバリングを1スタートに合わせる
>>> primelist.insert(0, 1) # 素数リストの先頭に要素1を追加
>>>
>>> # ファイル出力
>>> file = 'primelist_'+a+'_ko.binaryfile' # 生成するファイルのファイル名 primelist_10**4_ko.binaryfile
>>> file = file.replace('**', 'to_power') # ファイル名の**部分をリネーム primelist_10to_power4_ko.binaryfile
>>> f = open(file,'wb') # リストをファイルに書き出し
>>> pickle.dump(primelist, f) # データ上書き
>>>
>>> # 生成されたファイルを読み込み
>>> f = open(file,'rb')
>>> primelist = pickle.load(f)
>>> # 内容チェック
>>> # print(primelist) # コメントアウト:nが大なら非表示、コメント解除:nが小ならリスト全出力
>>> print('\nデータ数',len(primelist),'個') # 全要素数出力
>>> print('0番目', primelist[0]) # 0番目のデータ出力
>>> print('1番目', primelist[1]) # 1番目のデータ出力
>>> print('最後', len(primelist)-1,'番目',primelist[len(primelist)-1]) # 最後のデータ出力
>>> print(file,'\nが生成されました。') # 生成されたファイル名出力
このコードでは、いったん2,3,5,…と素数リストをつくった上で、最後にリストの先頭に1を追加しています。出来上がるファイルはコード3のものと同じです。
コード4 実行結果
数時間かけて10**8個(1億個)の素数リスト「primelist_10to_power8_ko.binaryfile」が出力されました。
出来上がるのは500MBのバイナリーファイルです。
テキストファイルではないのでダブルクリックして中身を直接見ることはできません。
コード5 「eulerproduct_zeta2_list.py」
いよいよ、コード4でつくった1億個の素数リストを使ってオイラー積の計算を行います。
バイナリーファイルprimelist_n_ko.binaryfile を読み込む場合も標準ライブラリpickleをインポートします。
>>> # eulerproduct_zeta2_list.py
>>> # ζ(2)=1.6449340668482264364724...のオイラー積による数値計算
>>> # 生成したn個の素数リスト primelist_n_ko.binaryfile を指定して使用
>>> # nを上限に、オイラー積の素数の個数を指定する
>>>
>>> from sympy import * # 数値計算 sympy.N()
>>> import pickle # ファイル読み込み pickle.load()
>>>
>>> # 任意精度演算 桁数設定
>>> from mpmath import mp
>>> mp.dps = 100 # 小数点以下100桁
>>>
>>> # ゼータ関数ζ(x) = mpmath.zeta(x)
>>> from mpmath import zeta
>>>
>>> print('ζ(2)=1.6449340668482264364724...のオイラー積による数値計算 素数リスト使用')
>>> a = input('読み込む素数リスト:primelist_n_ko.binaryfile のnを指定してください。例 1000や10**4など n >> ') # 1億個の素数リスト使用の場合は10**8
>>> file = 'primelist_'+a+'_ko.binaryfile' # primelist_10**8_ko.binaryfile
>>> file = file.replace('**', 'to_power') # fileの**をto_powerにリネーム primelist_10to_power8_ko.binaryfile
>>>
>>>
>>> # 作成した素数ファイルを読み込みリスト化する
>>> f = open(file,'rb') # primelist_10to_power8_ko.binaryfile を読み込む
>>> prime = pickle.load(f)
>>>
>>> # ノーマル演算 任意精度演算 mp.mpf()なし
>>> def eulerproduct0(N):
>>> P = 1
>>> for i in range(1, N):
>>> p = 1/(1-1/(prime[i]**2)) # mpf 不使用
>>> P = P * p
>>> return P
>>>
>>> # 計算精度を比較する場合には以下6行をコメントアウト
>>> # print('\nノーマル演算 任意精度演算 mp.mpf()なし')
>>> # print('ζ(2)=\t', N(zeta(2),30), '(真値)')
>>> # print('10コ\t', N(eulerproduct0(10), 30))
>>> # print('100コ\t', N(eulerproduct0(100), 30))
>>> # print('1000コ\t', N(eulerproduct0(1000), 30))
>>> # print('10^4コ\t', N(eulerproduct0(10000), 30))
>>>
>>>
>>> # 任意精度演算 mp.mpf()使用
>>> def eulerproduct(N):
>>> P = 1
>>> for i in range(1, N):
>>> p = 1/(1-mp.mpf('1')/(prime[i]**2)) # mpfはReal float用
>>> P = P * p
>>> return P
>>>
>>> # 読み込む素数リストの個数nを上限に、計算する素数の個数を指定
>>> # 1億個の素数リスト使用の場合には以下すべてをコメントアウト
>>> print('\n任意精度演算 mp.mpf()使用')
>>> print('ζ(2)=\t', N(zeta(2),30), '(真値)')
>>> print('10コ\t', N(eulerproduct(10), 30))
>>> print('100コ\t', N(eulerproduct(100), 30))
>>> # print('1000コ\t', N(eulerproduct(1000), 30))
>>> # print('10^4コ\t', N(eulerproduct(10000), 30))
>>> # print('10^5コ\t', N(eulerproduct(100000), 30))
>>> # print('10^6コ\t', N(eulerproduct(1000000), 30))
>>> # print('10^7コ\t', N(eulerproduct(10000000), 30))
>>> # print('10^8コ\t', N(eulerproduct(100000000), 30))
コード5を実行すると、「読み込む素数リスト:primelist_n_ko.binaryfile のnを指定してください。」ときかれます。
1000や10**4のようにコード3またはコード4でつくった素数リストの個数を入力します。1億個の素数リストを使う場合には10**8と入力します。
あとは、そのファイルが読み込まれ、オイラー積が計算されます。その際に、最後のコード部分のコメント#を調整して何個の素数まで計算するかを指定します。
>>> print('\n任意精度演算 mp.mpf()使用')
>>> print('ζ(2)=\t', N(zeta(2),30), '(真値)')
>>> print('10コ\t', N(eulerproduct(10), 30))
>>> print('100コ\t', N(eulerproduct(100), 30))
>>> # print('1000コ\t', N(eulerproduct(1000), 30))
>>> # print('10^4コ\t', N(eulerproduct(10000), 30))
>>> # print('10^5コ\t', N(eulerproduct(100000), 30))
>>> # print('10^6コ\t', N(eulerproduct(1000000), 30))
>>> # print('10^7コ\t', N(eulerproduct(10000000), 30))
>>> # print('10^8コ\t', N(eulerproduct(100000000), 30))
コード5 実行結果
1億個の素数リストを使ったオイラー積の計算結果です。

1番目の素数2から1億番目の素数2038074743までを用いたζ(2)のオイラー積の計算結果は、11桁の正しい値でした。
ぜひ自分のPCを使って素数リストをつくってみましょう。一度作っておくと素数を使った実験にいろいろと使えて便利です。
ゼータの数値計算の旅はつづきます。次回は電子計算機がなかった300年前、いかにしてオイラーがゼータを計算したのか、その秘密にPythonとともに迫ります。
