目次
集合とリストを比べる
前回は素数判定プログラム(prime1からprime 4)を紹介しました。
素数といえばエラトステネスの篩(ふるい)が有名なので、Pythonでエラトステネスの篩をコーディングすることを目指します。
そこで活躍するのがPythonによる集合の計算です。インタラクティブモードで確認していきます。
リストは[]を用いてデータを囲みます。データをインデックスで管理することができます。
>>> L = ['a', 'a', 'a', 'b', 'b', 'c']
>>> L
>>> ['a', 'a', 'a', 'b', 'b', 'c']
>>> L[0]
>>> 'a'
>>> L[5]
>>> 'c'
>>> print(type(L))
>>> <class 'list'>
それに対して、集合は{}を用いてデータを囲みます。上と同じデータを{}で囲んでみます。
>>> A = {'a', 'a', 'a', 'b', 'b', 'c'}
>>> A
>>> {'a', 'c', 'b'}
>>> print(type(A))
>>> <class 'set'>
これからわかるように、Pythonの集合は要素の重複を自動で排除してくれる便利な機能を持っています。
そして、{'a', 'c', 'b'}からわかるように、集合の要素には順序の情報が付随しません。
集合生成時に指定した順序とは異なる順番で集合の要素が出力されます。
空集合の生成
>>> P = {}
>>> print(P)
>>> {}
>>> print(type(P))
>>> <class 'dict'>
空集合は{}と思いきや、{}は辞書dict型となります。
空集合を生成するにはset()を用います。
>>> Q = set()
>>> print(Q)
>>> set()
>>> print(type(Q))
>>> <class 'set'>
たしかに集合set型です。
集合の生成
2つの集合を生成し、集合演算を確認してみます。和・差・積・対称差・一致・不一致・包含関係といった演算ができます。
先に生成した集合{'a', 'c', 'b'}はset()を用いてset('abc')とすれば生成できます。
>>> A = set('abc')
>>> B = set('bcde')
>>> print(A)
>>> {'a', 'c', 'b'}
>>> print(B)
>>> {'e', 'c', 'd', 'b'}

この集合AとBの和・差・積を計算してみます。
集合の和
2つの集合の和集合A∪B(AまたはB)は、A|Bで得られます。
>>> A|B
>>> {'a', 'c', 'e', 'd', 'b'}

集合の差
2つの集合の差集合は、A-Bで得られます。
>>> A-B
>>> {'a'}
>>> B-A
>>> {'d', 'e'}

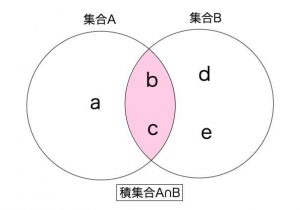
集合の積
2つの集合の積集合A∩B(AかつB)は、A&Bで得られます。
>>> A&B
>>> {'c', 'b'}
比較演算
Pythonには集合どうしの比較をする比較演算が装備されています。
次の3つの集合を準備します。
>>> A = set('ab')
>>> B = set('abcde')
>>> C = set('daecb')
>>> A
>>> {'a', 'b'}
>>> B
>>> {'a', 'c', 'e', 'b', 'd'}
>>> C
>>> {'c', 'a', 'e', 'b', 'd'}

集合Aと集合Bが等しいか否かを調べるにはA == Bとします。
>>> A == B
>>> False
集合Aと集合Bは完全一致(A == B)しないので、Falseが返されます。
>>> B == C
>>> True
集合Bと集合Cは完全一致(B == C)するので、Trueが返されます。
集合Aと集合Bの関係は「集合Aは集合Bの部分集合である」といい、A⊂Bと表します。
>>> A < B
>>> True
>>> B < A
>>> False
集合Bと集合Cの関係はB = Cです。
>>> B < C
>>> False
>>> B <= C
>>> True
通常、数学では「部分集合」という用語には等しい場合が含まれます。A=Bのとき、AはBの部分集合といいます(AはBに含まれるからです)。
上の計算から分かるようにPythonではB < CにB = Cは含まれないので、B<Cは部分集合B⊂Cを表しません。部分集合B⊂Cを判定するにはB<=Cとする必要があります。
次回はset()を用いて素数をリストアップするエラトステネスの篩をコーディングしてみます。
