これまで清少納言知恵の板、裁ち合わせ、魔方陣と江戸時代の正方形パズルを紹介してきました。
今回は世界が挑戦し続け解決された正方形の難問を紹介します。
目次
正方形分割正方形(Squared Square)|ルジンの問題
Squared Squareを訳すと、正方形分割された正方形(正方形分割正方形)です。
正方形を、すべて異なる大きさの正方形で重複も隙間もなく埋めることができるか?
ルジンの問題とも呼ばれるこの問題は、正方形がいかに美しく、いかに難しい存在かを物語ります。
今回は正方形分割正方形の歴史をたどっていきたいと思います。
面倒な解説ぬきに正方形分割正方形の絵を眺めていくだけで、その魅力は十分に感じてもらえるでしょう。
1902年、デュドニーの『カンタベリー・パズル』
1902年に出されたデュドニーの『カンタベリー・パズル』には114個のパズルが載っており、その40番目が“Lady Isabel's Casket”(イザベル夫人の小箱)という問題です。
イザベル夫人の宝物の一つが木で細工された小箱でした。小箱自体が正方形で、その中も正方形で仕切られているというものでした。
ただ、木箱の中には細長い黄金の細片(10インチ×1/4インチ)があるという条件が付いています。問題は、それがどういう形をした小箱かということです。
以下は解答ページにある図です。
正方形の真ん中の数は一辺の長さを表します。確かに一辺が20インチの正方形の内部がすべて異なる大きさの正方形で分割されています。真ん中部分には10インチ×1/4インチの長方形が確認できます。

『カンタベリー・パズル』の“イザベル夫人の小箱”(1902年)。正方形の真ん中の数は一辺の長さを表します。
デュドニーは、このパズルは細長い黄金の細片があるから解けるのであって、この条件なしにすべてを異なる正方形で埋め尽くすことは不可能であると言っています。
1903年に、デーンは次のことを証明しました。
長方形の辺の長さの比が有理数であることは、その長方形が正方形分割できるための必要十分条件である。
のちにこの定理が正方形分割正方形の解決の大きな突破口になることになろうとは、デーン自身思いもよらないことでした。
1917年、単純不完全正方形分割正方形
1917年、ロイドによって次の正方形分割が発見されました。

ロイドによる単純不完全正方形分割正方形(1917年)
同じ正方形があるので、これは“不完全完”な正方形分割(単純不完全正方形分割正方形:Simple Imperfect Squared Square)と呼ばれます。
1925年、正方形分割長方形
1925年、モロンは以下を発表しました。

モロンによる正方形分割長方形(1925年)
残念ながらこれは正方形ではありません。確かに異なる大きさの9つの正方形で分割されていますが、縦32、横33の長方形です。
正方形の完全正方形分割ができるかどうかすらわかっていなかった1931年に、安倍道雄は注目すべき研究を行いました。
長方形の正方形分割には9つの正方形が必要であること、そして異なる正方形で埋められるいくらでも正方形に近い長方形が存在することを明らかにしました。
1938年、完全正方形分割正方形
1938年、スプレーグは正方形の完全正方形分割を発見しました。
一辺が4205の正方形が、すべて異なる55個の正方形で埋め尽くされています。

スプレーグによる完全正方形分割正方形(1938年)
確かにこれは、それまでできないとされていた「正方形をすべて異なる正方形で埋め尽くす」を実現した記念すべき最初の例です。
しかし、これは正方形の中に2つの大きな長方形を見つけることができてしまう特殊な完全正方形分割です。
デュドニーの『カンタベリー・パズル』の問題にもあった制限がすべてなくなってはいない、あと一歩の答えでした。
1939年、単純完全正方形分割正方形
1939年、ついに制限をすべてなくした完全正方形分割がブルックスによって発見されました。一辺が4920の正方形を38個の正方形で埋め尽くしています。
先ほどのように、内部に長方形はありません。これを単純完全正方形分割正方形(Simple Perfect Squared Square)といいます。
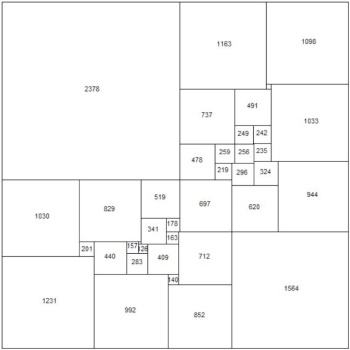
ブルックスによる単純完全正方形分割正方形(1939年)
次回後編では、単純完全正方形分割正方形の最終解答と驚異の日本人が登場します。
