三目並べで学ぶ強化学習｜Q学習と実装例を解説（1） - 空間情報クラブ

強化学習は機械学習が研究され始めた初期の1950年代から存在し、歴史的には「教師あり学習」など他の機械学習手法の派生元に位置付けられる分野です。

最近では2016年に強化学習を用いたGoogle DeepMindの囲碁AI「Alpha Go」がトップ棋士に完勝するという成果を挙げて話題になりました。

この記事では強化学習の理論を簡単に紹介し、その基本例をTic-Tac-Toe（○×ゲーム、三目並べ）というゲームを用いた実装で確認します。

強化学習とは

強化学習（Reinforcement Learning）は機械学習（Machine Learning）の一つで、システムが自ら試行錯誤しながら最適な制御を実現する手法のことをいいます。

強化学習の理論

強化学習では環境とエージェントの相互作用を考えます。

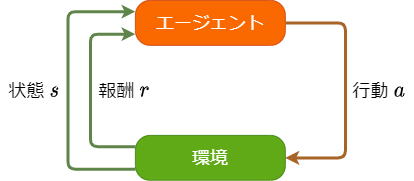
図1: エージェントと環境の相互作用

エージェントは環境の状態$s$を見て、行動$a$を実行します。環境はエージェントの行動$a$に応じて状態$s$を更新し、行動の結果として報酬$r$をエージェントに返します。

例えばブラックジャックのゲームでエージェントがプレイヤーの場合を考えると、状態は「表向きで表示されているトランプの数字」、行動は「ヒット・スタンドなどのプレイヤーが取れる選択肢」、報酬は「勝敗に応じた配当から賭け金を引いた値」とすることができます。

強化学習の目的は環境を攻略するエージェントを育てること、つまり総報酬がなるべく多くなる行動の選び方を模索することになります。

$$R_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \cdots = \sum_{k=1}^{\infty} \gamma^{k-1} r_{t+k}.$$

エージェントはその瞬間だけ報酬が高くなる行動を選ぶのではなく、長い目で見て得をする行動を選ぶことが求められます。

そのバランスを担うのが割引率と呼ばれるパラメーター$\gamma\in(0, 1)$です。$\gamma$を$1$に近付けるほど長期的な総報酬となり、逆に$0$に近付ければ瞬間的な総報酬となります。

状態が$s$のとき、エージェントは確率的に行動$a$を選択するとします。その確率分布を$\pi(s, a)$と表して方策と呼びます。方策を調整することで、より大きな総報酬を得られるようになれば目的が達成されます。

その方法を考えるために、状態価値関数$V^\pi(s)$と行動価値関数$Q^\pi(s, a)$という指標を導入します。

\begin{eqnarray}
V^\pi(s) &:=& E_\pi\{R_t | s_t = s\}, \\
Q^\pi(s, a) &:=& E_\pi\{R_t | s_t = s, a_t = a\}.
\end{eqnarray}

状態価値関数$V^\pi(s)$は状態が$s$であるときにエージェントが受け取れる総報酬の期待値で、行動価値関数$Q^\pi(s, a)$は状態が$s$であるときに行動$a$を取った場合にエージェントが受け取れる総報酬の期待値です。

このとき$R_t$の定義より、$V(s)$と$Q(s, a)$の間に次の関係が成立します。

\begin{eqnarray}
V^\pi(s) &=& \sum_{a} \pi(s, a)Q^\pi(s, a), \\
Q^\pi(s, a) &=& \sum_{s'} P_{s, s'}^{a}\left( R_{s, s'}^{a}+\gamma V^\pi(s')\right) .
\end{eqnarray}

これをBellman方程式と呼びます。ここで、$P_{s, s'}^{a}$は状態$s$で行動$a$を取ったときに状態が$s'$に遷移する確率、$R_{s, s'}^{a}$は状態$s$で行動$a$を取ったときの報酬の期待値です。

これに対して、最大の状態価値関数・行動価値関数を達成する方策$\pi^*$が存在することが証明されています。このとき、$V^*:=V^{\pi^*}, Q^*:=Q^{\pi^*}$に対して次の関係が成立します。こちらはBellman最適方程式と呼ばれます。

\begin{eqnarray}
V^*(s) &=& \max_{a} Q^*(s, a), \\
Q^*(s, a) &=& \sum_{s'} P_{s, s'}^{a}\left( R_{s, s'}^{a}+\gamma V^*(s')\right) .
\end{eqnarray}

最善の選択をするエージェントを求めるという強化学習の目的は、数学的に言い換えるとBellman最適方程式を解くことになることがわかりました。

Q学習

Bellman最適方程式の解法には動的プログラミング・モンテカルロ法・TD学習などの様々な手法がありますが、今回はその中でもTD学習に属する「Q学習」を使います。

TD学習(Temporal-Difference Learning)はモデルに関する情報($P_{s, s'}^{a}$と$R_{s, s'}^{a}$)が不要で、行動1回単位で価値関数を更新できるという特徴があります。

Q学習では名前の通り行動価値関数$Q$を更新していきます。状態$s_t$で行動$a_t$を取ったときに報酬$r_{t+1}$が得られて状態が$s_{t+1}$に遷移したとき、$Q$の値を次のように更新します。

$$
Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( r_{t+1} + \gamma \max_{a}Q(s_{t+1}, a) - Q(s_t, a_t)\right).
$$

ここで$\alpha$は学習率です。この更新式は変形すると以下のようになります。

$$
Q(s_t, a_t) \leftarrow (1-\alpha)Q(s_t, a_t) + \alpha \left( r_{t+1} + \gamma \max_{a}Q(s_{t+1}, a)\right).
$$

更新を行う度に$Q(s_t, a_t)$の値が$r_{t+1} + \gamma \max_{a}Q(s_{t+1}, a)$に$\alpha$の割合で近づくという式になります。

$r_{t+1} + \gamma \max_{a}Q(s_{t+1}, a)$はBellman最適方程式の中に現れる$R_{s, s'}^{a}+\gamma V^*(s')$に対応しており、この更新を繰り返すことで$Q$は$Q^*$に近付いていきます。

目的の方策は$Q$を用いて次のように求められます。

\[
\pi(s, a) =
\begin{cases}
1 & (a = \underset{a}{{\rm argmax}}Q(s, a)), \\
0 & ({\rm otherwise}).
\end{cases}
\]

$Q$の更新が局所に偏らないように、学習時に取る行動$a_t$はε-greedy法などを使って多少のランダム性を加えて選びます。

実装: Tic-Tac-Toe

実装では$Q$を配列で表現して、全ての$(s, a)$に対応する$Q$の値を保持します。そのため、可能な状態や行動の数が膨大な問題では、必要なメモリーの容量や収束までの計算量が爆発してしまい向いていません。

今回扱うTic-Tac-Toe(○×ゲーム、三目並べ)というゲームは、状態の数が高々$3^9=19683$通り、行動の数が$9$通りなのでQ学習で十分学習可能です。

Tic-Tac-Toe

Tic-Tac-Toeのルールを以下のように定めます。

盤面は縦横3マスずつの9マス
最初は全てのマスが空の状態
先手は×を、後手は○を交互に空のマスに書き込んでいく
パスは不可
自分のマークを縦横斜めのいずれか一列で3つ並べた方が勝ち
勝敗が決せずに9マス全てが埋まったら引き分け

実装

状態$s$は盤面の状態に対応していて、行動$a$は次に書き込む位置に対応しています。

報酬$r$は勝敗の結果に対応していて、今回は勝ったときに$1$、負けたときに$-1$、勝敗がついていないときは常に$0$となるように設定します。

状態遷移

ここで注意しなければならないのは、Tic-Tac-Toeは先手と後手が交互にプレイするゲームであるということです。

したがって図2のように、先手から見て状態$s_t$の次の状態$s_{t+1}$は$s_t$に$a_t$を反映させた直後の状態$s'_t$ではなく、次の相手の行動$a'_t$の後の状態となります。

図2: Tic-Tac-Toeの状態遷移

Q学習では同じエージェント同士のゲームで$(s_t, a_t, r_{t+1}), (s'_t, a'_t, r'_{t+1})$を取得し、$(s_t, a_t, r_{t+1}-r'_{t+1}, s_{t+1})$あるいは$(s'_t, a'_t, r'_{t+1}-r_{t+2}, s'_{t+1})$で行動価値関数$Q$を更新するという操作を繰り返します。

afterstate

図2のように、Tic-Tac-Toeでは状態$s_t$に行動$a_t$を作用させた結果は確率によらず常に$s'_t$となります。

このように行動に対する結果が予めわかっている場合その結果をafterstateと呼び、図2の例の場合では$s'_t = afterstate(s_t, a_t)$と表します。

このとき行動価値観数$Q$は、状態と行動の対$(s, a)$を$afterstate(s, a)$に集約することで、$Q(s, a) = Q(afterstate(s, a))$と1変数関数として表現することが可能になります。

こうすることで$Q$が占有するメモリ領域を狭められるほか、図3のように同じafterstateになる複数の行動に対する行動価値をひとまとめに管理できるようになり学習効率も上がります。

図3: Tic-Tac-Toeにおけるafterstateの例

実験

Q学習で実装した同じエージェントどうしの5万回のゲームで学習しました。パラメーターはそれぞれ割引率を$\gamma=0.9$、学習率を$\alpha=0.1$、ε-greedy法の定数を$\varepsilon=0.5$としました。

学習回数に対するエージェントの変化を以下のグラフで示します。青が勝ち、橙が引き分け、緑が負けの割合を意味しています。

上段はランダムに手を選ぶエージェントと1000回対戦した結果で、下段は学習したゲーム回数が500回前の過去のエージェントと1回対戦した結果です。左は自分が先手で、右は対戦相手が先手のときの結果になります。

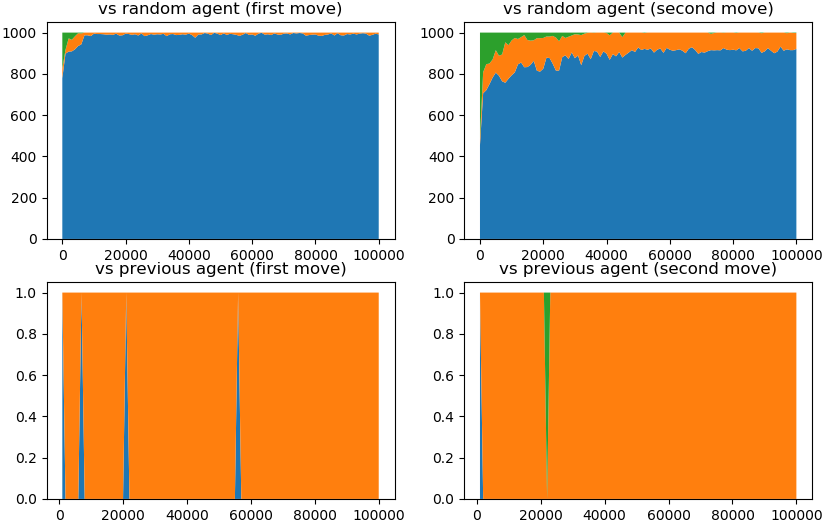
図4: 実験結果

ランダムなエージェントとの対戦結果を見ると学習の初期で既に負けはなくなり、安定した勝率が得られていることがわかります。また、過去のエージェントとの対戦を見ても最初を除いて全て引き分けとなっており安定しています。

過去のエージェントとの対戦で勝ちが現れないのは、エージェントの学習が同じエージェント同士の対戦で行われることから、エージェントが選びやすい手の学習がランダムに選ばれる手よりも早く進んでいることが要因として考えられます。

ソースコード

Pythonで実装したソースコードを以下の場所で公開しています。

informatix-inc/q-tic-tac-toe: 強化学習(Q学習)でTic-Tac-Toeを攻略する実装例

save/tic_tac_toe_qは100万ゲーム学習した結果です。tic_tac_toe_demo.pyを実行すれば学習されたエージェントとコンソール上で対戦することもできます。

図5: 学習されたエージェントと対戦

まとめ

第1回は強化学習の基礎と、Tic-Tac-Toeを用いたQ学習の実装例を紹介しました。

Tic-Tac-Toeは非常に単純なゲームで、強化学習を使わなくても少し考えれば最適な戦略を見つけることができます。

次回は戦略を見つけることが少し難しいゲームに強化学習を適用してその動きを確かめます。

物体検出などAI機械学習を活用したシステムの構築に関するご相談（無料）を承っています

お気軽にお問い合わせください

参考文献

[1] Richard S. Sutton and Andrew G. Barto (2018). Reinforcement Learning: An Introduction. The MIT Press A Bradford Book.