Transformerを採用した最新の物体検出手法｜DETR

こんにちは、インフォマティクスで機械学習業務を担当している大橋です。

今回は物体検出技術の紹介をしたいと思います。

ここで紹介する論文[1]は、これまでと異なるアプローチにより、既存モデルの問題点を解消した大変興味深い内容となっています。

※本記事はTransformer [5]等の深層学習の知識がある程度あることを前提として書いています。

物体検出とは

物体検出とは、画像の中から物体の位置を矩形で予測し、その物体が何であるかを推定する問題のことをいいます。

物体検出の例（論文[1]より抜粋）

これまでの物体検出手法

物体検出という問題に対して、これまで様々な手法が提案されてきました。

物体の候補領域の推定とクラスの推定をそれぞれ2つの独立したネットワークで行うもの(two stage detector)[2]や、それらを1つのネットワークで同時に推定するもの(one stage detector)[3,4]が代表的です。

実はこれまでの手法には望ましくない点が2つあります。

一つは同じような物体候補領域をたくさん予測してしまう点です。予測の重複を取り除くためにはnon-maximal suppression（以下、NMS）と呼ばれる事後処理が必要です。

もう一つは、あらかじめAnchor等の候補領域の大きさ等を設定しておく必要がある点です。

物体の大きさのような事前知識を用いるのはカンニングであり好ましくありません。また、これらの設定値によって精度が大きく変わることがあるため、できれば学習で自動的に獲得するのが望ましいのです。

事前知識の利用や事後処理を行わない、いわゆるEnd-To-Endな学習は機械翻訳や音声認識等の分野では大きな成果をあげていましたが、物体検出ではまだ取り入れられていませんでした。

同じような物体候補領域をたくさん予測してしまう原因は、各々の領域を予測する際に他の予測内容を考慮していないことにあります。

他に予測された物体であれば、もうその部分は予測する必要はありません。つまり、各予測が他の予測内容を観察して忖度できるようになればこの問題は解消されます。

詳しい人はこの時点でピンとくるかもしれませんが、注意機構をネットワーク内に上手く取り入れて他の予測内容が垣間見られるようになれば解決しそうな気がします。

注意機構を上手く物体検出に取り入れることにより、NMSのような事後処理を排除し、End-To-Endな学習を可能にした手法が今回の論文[1]で提案されたモデル"Detection Transformer"（以下、DETR）です。

DETRの概要

DETRは非常に分かりやすい構造をしています。構成要素は以下の3つです。

• Backbone：画像の特徴量をエンコードするためのCNNネットワーク
• Transformer：CNNから取り出された画像の特徴量から注意機構を用いて各物体の位置や種類の情報へと変換。事前に決められた個数Nの物体を予測します。他の予測内容を見て自身の予測を忖度するEncoder-Decoderネットワーク
• FFN：Transformerの出力を物体の位置座標・クラスラベルにデコードするネットワーク

全体像は以下になります。

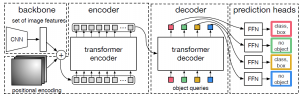
図1：DETRの全体像（論文[1]から抜粋）

Backboneは画像の特徴量を低次元にエンコードできれば何でもよいのですが、論文ではResNet [6]を用いています。

Backboneへの入力のテンソルの形は、画像サイズを\((H_{in}, W_{in})\) とすると\(\mathbb{R}^{3 \times H_{in} \times W_{in}}\)で、出力は画像サイズを\((H_{out}, W_{out})\)、チャンネル数を\(C_{out}\) とすると\(\mathbb{R}^{C_{out} \times H_{out} \times W_{out}}\)です。今回は\(H_{out}=H_{in}/32\)、\(W_{out}=W_{in}/32\)、\(C_{out}=2048\)としています。

Transformerへはそのまま入力できないため、Backboneの出力\(\mathbb{R}^{C_{out} \times H_{out} \times W_{out}}\)に\(1 \times 1\)の畳込層でチャンネル数を\(d\)に圧縮後、\(\mathbb{R}^{d \times H_{out}W_{out}}\)にreshapeしたものを入力とします。

FFNは3層の畳込み+ReLUと最後に線形変換を加えたものです。

様々な工夫

DETRは学習の際に様々な工夫をしています。

以下では物体の予測の順不同性を保証する工夫（①）、計算量を抑える工夫（②）、小さな物体の検出精度を上げる工夫（③）を解説します。

① Hungarian Loss

提案モデルはTransformerの出力順序に応じて「1番目の物体の位置は○○でクラスは××、2番の物体はの位置は~」というようにN番目まで予測します。

全くとは言い切れませんが、物体の存在する位置やクラスには相関はなく順序は関係ないはずです。つまり、順序は違うが予測内容が同じであれば訓練時の損失は同じであることが望ましいです。

損失関数を予測の順序に対し不変にするためにHungarian Lossというものを導入しています。やっていることはとても自然で、予測と正解を比べて最も当てはまりの良いペアを見つけて、それらに対して損失をとるというものです。

最も当てはまりの良いペアを見つける操作を数式で表すと以下になります。

\( \hat{\sigma} = {\rm arg~min}_{\sigma \in \mathcal{Q_N}}\sum^{N}_{i}\mathcal{L}_{match}(y_{i},\hat{y}_{\sigma_{(i)}})\)

\(\mathcal{Q_N}\)がN次の置換群、\(\{y_{i}\}_{i=1}^{N}\)が正解、\(\{\hat{y}_{i}\}_{i=1}^{N}\)がネットワークの予測です。正解数がN以下の場合は該当クラス無しを意味する\(\emptyset\)で埋めています。\(y_{i}=(c_{i},b_{i})\)で\(c_{i}\)が正解のクラス、\(b_{i}\)は正解のボックス位置・サイズで\(b_{i}\in [0,1]^4\)です。予測も同様です。\(\mathcal{L}_{match}(y_{i},\hat{y}_{\sigma_{(i)}})\)は以下で定義されます。

\(\mathcal{L}_{match}(y_{i},\hat{y}_{\sigma_{(i)}})=-\mathcal{1}_{\{c_i\neq \emptyset \}}\hat{p}_{\sigma_{(i)}}(c_{i})+\mathcal{1}_{\{c_i\neq \emptyset \}}\mathcal{L}_{box}(b_{i},\hat{b}_{\sigma_{(i)}})\)

\(\mathcal{1}_{\{c_i\neq \emptyset \}}\)は該当クラス無しの部分は0,それ以外は1という意味です。\(\hat{p}_{\sigma_{(i)}}(c_{i})\)は正解クラスの予測確率です。\(\mathcal{L}_{box}(b_{i},\hat{b}_{\sigma_{(i)}})\)は位置に対する予測確率で詳細は③で定義します。

このように見つけた正解と予測のペアに対して、以下の操作で順不同な損失関数\(\mathcal{L}_{hungarian}\)を構成しています。

\(\mathcal{L}_{hungarian}(y,\hat{y})=\sum_{i=1}^{N}\left[-\log \hat{p}_{\hat{\sigma}_{(i)}}(c_i)+\mathcal{1}_{\{c_i\neq \emptyset \}}\mathcal{L}_{box}(b_{i},\hat{b}_{\hat{\sigma}_{(i)}})\right]\)

② Parallel Decoding

オリジナルのTransformerのデコーダは、「一つ単語を予測し、その出力を入力にしてまた次の単語を予測」といったことを逐次的に行い予測をしていました。しかし、これは計算量が膨大になります。

そこで、逐次的ではなく一回の順伝播のみで予測を行っています(Parallel Decoding)。予測を行う際は図1にあるように、object queryと呼ばれる固定長のテンソルを入力とします。このobject query自身も学習対象です。

これまでの物体検出でもそうなのですが、固定長のobject queryを入力するため予測できる物体の個数の上限が決まってしまっています。

その固定長は、通常の画像に写り込んでいる物体の数よりも十分に大きくとる必要があります。ここで事前知識を用いています。

③ Generalized IoU Loss

物体予測位置に対する損失としてGeneralized IoU(以下、GIoU)を用いたものを導入しています。

通常は\(\mathcal{L}^p\)損失を用いますが、この場合大きな物体に対しては損失が大きくなり小さな物体に対しては損失が小さくなってしまう傾向があります。

そのため、小さな物体の検出精度が低くなってしまうという問題があります。このようなスケール依存性を小さくするために導入されています。

GIoUとは矩形領域A、矩形領域Bがあったときにその2つを囲う最小の矩形領域Cを導入し、これら3つの領域に対して以下のように定義します。

\(GIoU(A,B) = \frac{|A\cap B|}{|A\cup B|}-\frac{|C\setminus (A\cup B)|}{|C|}\)

GIoUは\(|A\cap B|=0\) の場合にも集合の離れ具合を評価できるようにしたものです。このGIoUに対して、GIoU Loss \(\mathcal{L}_{giou}(A,B)\)を以下のように定義します。

\(\mathcal{L}_{giou}(A,B)=1-GIoU(A,B)\)

本論文では、GIoU Lossに加え\(\mathcal{L}^{1}\)損失を加えたものを位置に対する損失関数としています。最終的には\(\lambda_{giou},\lambda_{L1}\)を定数として以下になります。表記は①と同様です。

\(\mathcal{L}_{box}(b_i,\hat{b}_{\sigma_{(i)}})=\lambda_{giou}\mathcal{L}_{giou}(b_i,\hat{b}_{\sigma_{(i)}})+\lambda_{L1}||b_i-\hat{b}_{\sigma_{(i)}}||_{1} \)

精度比較

今回比較対象としてFaster RCNN [2]を用いています。

DETRとフェアな比較を行うために、Faster RCNNもGIoU Lossの追加、学習データの拡張、長い学習を行うことにより、スタンダードなものより高精度になっています。

結果は以下の表1になります。

表1：論文[1]から抜粋

Faster RCNN（表1：中段）に比べて、全体としてDETRの精度は向上しています（表1：下段）。より詳細に見ると、大きな物体に対しては大きく精度(\(AP_{L}\))が向上しており、小さな物体の検出精度(\(AP_{S}\))は低いことが分かります。

各コンポーネントの影響度

論文では、各構成要素が精度にどのような影響があるのか詳細に調べています。

① TransformerのEncoderとDecoderのレイヤ数による影響

TransformerのEncoderとDecoderのレイヤ数を独立に変更して精度にどのような影響があるか調べています。

Encoderのレイヤ数は12層までは多ければ多いほど良いという結果です（表2）。

Decoderに関しては6層は固定で中間層の出力を使って予測を行った場合の精度を観察しています。こちらも6層まではレイヤ数が多ければ多いほど良いという結果になっています（図2）。

こちらの図ではNMSの効果も同時に測定しているのですが、層を増やすほどNMS効果がなくなっていき、6層の時はほとんど精度向上しないことが確認できます。

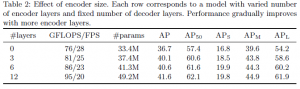
表2：論文[1]から抜粋

図2：論文[1]から抜粋

② Positional Encodingの影響

Transformerへの入力の際にreshapeを行っているため、画像の位置情報が失われてしまっています。そのためPositional Encodingは重要です。

どの程度重要なのかを調べたのが表3になります。特に全てのPositional Encodingを無くした場合に致命的な精度悪化を招くことが分かります。

また、意外なことに学習対象にしてしまうと精度が低下することも分かります。結果固定のPositional Encodingをbaselineとして採用しています。

表3：論文[1]から抜粋

③ GIoUの影響

GIoU lossの導入理由は小さな物体の認識精度を改善するためでしたが、どの程度の影響があるのか気になるところです。

実際に調べてみた結果が表4になります。小さな物体の精度に関してはかなりの効果があることが分かります。

表4：論文[1]から抜粋

おわりに

今回は物体検出の最新手法を紹介しました。これまでとは違った視点で物体検出に取り組んだ面白い論文でした。

DETRは色々な工夫がなされていますが、小さい物体の検出が苦手なようです。

また、本文では述べませんでしたが、学習に時間がかかるようです。これらの弱点の克服は今後の研究に期待したいところです。

論文[1]ではより詳細な解析がなされていますので、気になる方はそちらを参照してください。

参考文献

[1]Carion, N., Massa, F., Synnaeve, G., Usunier, N., Kirillov, A., & Zagoruyko, S. (2020). End-to-End Object Detection with Transformers. ArXiv, abs/2005.12872.

[2]Ren, S., He, K., Girshick, R.B., & Sun, J. (2015). Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence, 39, 1137-1149.

[3]Lin, T., Goyal, P., Girshick, R.B., He, K., & Dollár, P. (2017). Focal Loss for Dense Object Detection. 2017 IEEE International Conference on Computer Vision (ICCV), 2999-3007.

[4]Tian, Z., Shen, C., Chen, H., & He, T. (2019). FCOS: Fully Convolutional One-Stage Object Detection. 2019 IEEE/CVF International Conference on Computer Vision (ICCV), 9626-9635.

[5]Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A.N., Kaiser, L., & Polosukhin, I. (2017). Attention is All you Need. ArXiv, abs/1706.03762.

[6]He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 770-778.