ジョン・ネイピア対数誕生物語

ネイピアとの出会い

ジョン・ネイピア。

その名は世界でもあまり知られていません。しかし、彼の発見と発明は現代の私たちを支えています。

日々私たちが使っている小数点はネイピアの発明なのです。小数点は雨や雪のごとく天が降ってきたのではなく、ネイピアが対数を生み出す過程で考え出した副産物だったのです。

なぜネイピアは対数を考え出したのか。

それはネイピアが「計算」に対して異常なまでの執着心を持っていたからです。ネイピアは「ネイピアの計算棒」と呼ばれる計算機も発明しています。

ではなぜネイピアは計算にこだわったのでしょうか。それは当時の天文学がおかれた状況が関係していました。

その続きを語る前に、私とネイピアとの出会いがありました。高校2年生、数学の教科書で指数を対数に書き換えることを習いました。

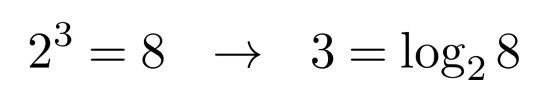そのとき「何のためにわざわざ指数の式2³=8を書き換える必要があるのか」と全く理解できませんでした。

そんなある日の放課後、図書館で1冊の数学書を見つけました。『100人の数学者』（日本評論社、1971年初版）。

手に取り頁をめくって斜め読みしていくと、「ネイピア」の頁で目がとまりました。「対数」の二文字が飛び込んできたからです。ちょうどlogに怒り心頭だったタイミングでした。

なぜ対数は生まれたのか

大航海時代、未熟な航海術のせいで船乗りの命が大海原の藻屑となっていました。

航海術に必要とされる天文学は、天文学者が行う天文学的計算によって支えられていましたが、天文学者は計算の呪縛に苦しめられていました。

そんな中、突如現れた対数という画期的計算術のおかげで天文学的計算が克服されていった、と記されていました。

私にとってそれはまさに驚くべき記述でした。「何のために対数はあるのか」の問いの答えが「人の命を救うため」だったからです。

ネイピアの生い立ち

ネイピアは、1550年、宗教戦争が続くスコットランドに生まれました。時代はヨーロッパ列強諸国が覇権を争う大航海時代の真っ只中。

ネイピアはマーキストン城の城主として官の仕事のほか、領民のために農業土木、軍事技術など多くの発明を行うエンジニアとして活躍する一方、熱烈なプロテスタントとして深い信仰を持つ人でもありました。

遠洋航海に必要な天文学（船の測位）を支える数学が球面三角法です。

驚くべきことにネイピアは「ネイピアの公式」という球面三角法の基本公式を発見しています。

これだけでも数学史に残る価値ある業績です。しかし、数学者でも天文学者でもないネイピアは現実の切実な問題解決を目標としていました。

それが天文学的計算の克服だったのです。

航海は計算との闘い

三角関数の計算の中に現れる大きい数の計算は天文学者を苦しめました。大航海時代は計算との闘いでもあったのです。

天文学者は直面する天文学的計算を克服する手立てを見つけることができませんでした。彼らの計算を助けるために、ネイピアはついに新しい計算法を見つけ出す決心をします。

1594年、時にネイピア44歳。その20年後の1614年、ついに人類は青天の霹靂として「対数」を手にします。

『Mirifici Logarithmorum Canonis Descriptio』(ラテン語、奇跡の対数法則の記述)
『Description of the wonderful canon of logarithms』(英訳、驚異の対数法則の記述)

ロガリズムという言葉は、この時ネイピアによって考案された造語です。logos（神の言葉）とギリシャ語のarithmos（数）を合わせてlogarithmsという言葉を作りました。

ネイピアは自らの著書を「奇跡」と呼びました。対数が「人の命を救う」だけの力を持っていると考えたからでしょう。

ネイピア対数とは

対数の考え方はいたってシンプルです。下の表は2の累乗を表したものです。

4×8＝32というかけ算は4と8が2を何回かけ算したかを考えるとそれぞれ2回、3回なので2回＋3回＝5回として表から5回の結果が32とわかる仕組みです。

すなわち、「対数とは2を何回かけたのかという回数」と考えられるということです。

2つの数の積を計算する場合、それぞれの回数（対数）を調べてそれらの和を求め、その和に対する累乗がさらに表からわかるということです。

この2のことを「底」と呼びます。つまりあらかじめこのような数表を作っておけば、かけ算はたし算と数表を調べればできてしまうということです。

さてネイピアが考えていたかけ算とは三角関数どうしのものです。ネイピアは1°刻みの角度に対する8桁の三角関数に対する8桁の対数を20年かけて作ったのです。

ここで重要なことは当時、指数表記と小数点がなかったということです。現在の2³という表記が考案されるまでには、ネイピアから100年以上もかかることになります。

驚くべきことにネイピアは指数も小数点もない時代に対数表を作り上げたのです。現代科学はこの2つなしに数値を表記することは不可能です。

ネイピア対数の底のふしぎ

ところで、ネイピアの対数の底は0.9999999という不思議な数でした。

この不思議な数は後に一人の天才によって謎が解かれ、そこから微分積分という新しい道が開けていくことになります。

ネイピアの対数表は8桁ですが、その計算精度を調べてみると7桁までは合っていることがわかります。

それでもこの本は人々に全く理解されませんでした。指数も小数点もないことに加えて、不思議な「底」のせいです。

しかしたった一人、天文学者ブリッグスがその本質を見抜き、1615年ネイピアに会いにマーキストン城に行きました。

ブリッグスがネイピアに対数の問題点をたずねると、なんとネイピアは既に新しい対数を考え始めていたのです。底が10の常用対数です。

翌年1616年、現在の常用対数が二人の手によって完成しました。ブリッグスはこの常用対数表の作成をネイピアと約束し、7年を費やしそれを果たしました。

しかしこの時、既にネイピアはこの世にはいませんでした。ネイピアとその対数は忘れ去られ、ブリッグスの対数表が世界を席巻することになりました。

数学者ラプラスをして「対数は天文学者の寿命を倍に延ばした」と言わしめました。

2006年、私に奇跡が起きました。ネイピアの原書を手にしたのです。

京都大学にひっそりと眠っていた原書が、偶然が重なり私のもとに届けられるという信じられない出来事が起きたのです。それが次の写真です。

『Mirifici Logarithmorum Canonis Descriptio』(奇跡の対数法則の記述)

書名に「奇跡」を入れ込んだネイピアの対数は、その後の数学に奇跡を起こし続けることになります。

対数なしに科学の発展はあり得なかったと言っても過言ではありません。

「ネイピアの対数」は忘れ去られてしまいました。しかし、現在から対数を振り返るとき、ネイピアの偉業と数学の力を確信した彼の思いが見えてきます。

次回は、ネイピアが対数表を作り上げる過程で発明された小数点「・」がどのように生まれたか、その誕生物語をご紹介します。

世界を変えた十大数学公式のうち3つに対数